Question

【题目】如图，在边长为4的正方形ABCD中，对角线AC，BD相交于点O，点E是AD边上一点，连接CE，把△CDE沿CE翻折，得到△CPE，EP交AC于点F，CP交BD于点G，连接PO，若PO∥BC，则四边形OFPG的面积是 ．

Answer 1

【答案】8﹣4
【解析】解：如图所示，过P作PM⊥AO于M，作PN⊥BO于N，延长PO交CD于H，

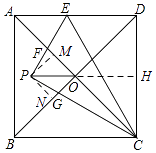
∵PO∥BC，BC⊥CD，

∴PH⊥CD，

又∵△CDO是等腰直角三角形，

∴OH= CD=2=CH，OH平分∠COD，

由折叠可得，CP=CD=4，

∴Rt△PCH中，PH= =2 ，

∴PO=PH﹣OH=2 ﹣2，

∵PO平分∠AOB，PM⊥AO，PN⊥BO，

∴PM=PN，

矩形PMON是正方形，

∴正方形PMON的面积= OP2= （2 ﹣2）2=8﹣4 ，

∵∠FPG=∠MON=90°，

∴∠FPM=∠GPN，

在△PMF和△PNG中，

，

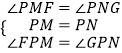∴△PMF≌△PNG（ASA），

∴S△PMF=S△PNG，

∴S四边形OFPG=S正方形PMON，

∴四边形OFPG的面积是8﹣4 ，

所以答案是：8﹣4 ．

【考点精析】利用等腰直角三角形和勾股定理的概念对题目进行判断即可得到答案，需要熟知等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．