【题目】今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外.如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75![]() 海里.
海里.
(1)求B点到直线CA的距离;
(2)执法船从A到D航行了多少海里?(结果保留根号)

参考答案:
【答案】执法船从A到D航行了(75﹣25![]() )海里.
)海里.
【解析】试题分析:(1)过点B作BH⊥CA交CA的延长线于点H,由已知可得∠BCA =30°,
利用30°角所对直角边等于斜边的一半即可求得BH的长,即B点到直线CA的距离;
(2)由BD、BH的长利用勾股定理可得DH的长,在Rt△ABH中,利用tan∠BAH=![]() 求得AH的长,从而可得AD的长.
求得AH的长,从而可得AD的长.
试题解析:(1)过点B作BH⊥CA交CA的延长线于点H,
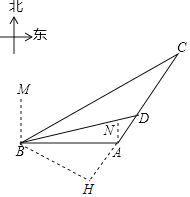
∵∠MBC=60°,
∴∠CBA=30°,
∵∠NAD=30°,
∴∠BAC=120°,
∴∠BCA=180°﹣∠BAC﹣∠CBA=30°,
∴BH=BC×sin∠BCA=150×![]() =75(海里),
=75(海里),
答:B点到直线CA的距离是75海里;
(2)∵BD=75![]() 海里,BH=75海里,
海里,BH=75海里,
∴DH=![]() =75(海里),
=75(海里),
∵∠BAH=180°﹣∠BAC=60°,
在Rt△ABH中,tan∠BAH=![]() =
=![]() ,
,
∴AH=25![]() ,
,
∴AD=DH﹣AH=(75﹣25![]() )(海里).
)(海里).
答:执法船从A到D航行了(75﹣25![]() )海里.
)海里.
-
科目: 来源: 题型:
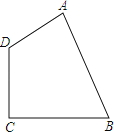
查看答案和解析>>【题目】如图,是一块四边形绿地的示意图,其中AB长为24米,BC长15米,CD长为20米,DA长7米,∠C=90°,求绿地ABCD的面积.
-
科目: 来源: 题型:
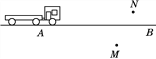
查看答案和解析>>【题目】如图,M,N为坐落于公路两旁的村庄,如果一辆施工的机动车由A向B行驶,产生的噪音会对两个村庄造成影响.
(1)当施工车行驶到何处时,产生的噪音分别对两个村庄影响最大?在图中标出来.
(2)当施工车从A向B行驶时,产生的噪音对M,N两个村庄的影响情况如何?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在Rt△ABC中,∠C=90°,有一内接正方形DEFC,连接AF交DE于G,若AC=15,BC=10.
(1)求正方形DEFC的边长;(2)求EG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=kx+b与反比例函数y=
 (x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.(1)求直线AB的解析式;
(2)若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】中华商场将进价为40元的衬衫按50元售出时,每月能卖出500件,经市场调查,这种衬衫每件涨价4元,其销售量就减少40件.如果商场计划每月赚得8000元利润,那么售价应定为多少?这时每月应进多少件衬衫?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)根据下列叙述填依据:
已知:如图①,AB∥CD,∠B+∠BFE=180°,求∠B+∠BFD+∠D的度数.
解:因为∠B+∠BFE=180°,
所以AB∥EF( ).
又因为AB∥CD,
所以CD∥EF( ).
所以∠CDF+∠DFE=180°( ).
所以∠B+∠BFD+∠D=∠B+∠BFE+∠DFE+∠D=360°.
(2)根据以上解答进行探索:如图②,AB∥EF,∠BDF与∠B,∠F有何数量关系?并说明理由.
(3)如图③④,AB∥EF,你能探索出图③、图④两个图形中,∠BDF与∠B,∠F的数量关系吗?请直接写出结果.

相关试题

