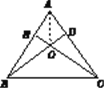
【题目】已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的平分线上,并说明理由.

参考答案:
【答案】见解析
【解析】(1)由OB=OC,即可求得∠OBC=∠OCB,又由,锐角△ABC的两条高BD、CE相交于点O,根据三角形的内角和等于180°,即可证得△ABC是等腰三角形;
(2)首先连接AO并延长交BC于F,通过证△AOB≌△AOC(SSS),得到∠BAF=∠CAF,即点O在∠BAC的角平分线上.
(1)证明:∵OB=OC
∴∠OBC=∠OCB
∵BD、CE是△ABC的两条高
∴∠BDC=∠CEB=90°
又∵BC=CB
∴△BDC≌△CEB(AAS)
∴∠EBC=∠DCB
∴AB=AC
∴△ABC是等腰三角形.
(2)解:点O在∠BAC的平分线上.如图,连接AO.
∵ △BDC≌△CEB
∴BD=CE
又∵OB=OC
∴OD=OE.
又∵∠BDA=∠CEA=90°
AO=AO
∴Rt△ADO≌Rt△AEO(HL)
∴∠DAO=∠EAO
∴点O在∠BAC的平分线上.
((2)也可用角平分线性质定理的逆定理,更简单)
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程2a-3x=6的解是非负数,那么a满足的条件是( )
A.a>3
B.a≤3
C.a<3
D.a≥3 -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2x﹣1>3的解集( )
A.x>1
B.x>﹣2
C.x>2
D.x<2 -
科目: 来源: 题型:
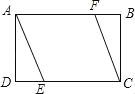
查看答案和解析>>【题目】(2016浙江省舟山市第9题)如图,矩形ABCD中,AD=2,AB=3,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是( )
A.
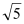 B.
B.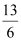 C.1 D.
C.1 D.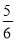
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个长方形的宽为a,长比宽的2倍少1.
(1)写出这个长方形的周长;
(2)当a=2时,这个长方形的周长是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,若直线y=kx+b经过第一,三,四象限,则直线y=bx+k不经过的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2x﹣4≥0的解集是 .
相关试题

