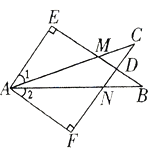
【题目】如图,在△ABE和△ACF中,EB交AC于点M,交FC于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF.下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中,正确的是_________.(填序号)
参考答案:
【答案】①②③
【解析】
∠E=∠F=90°,∠B=∠C,AE=AF可得△ABE≌△ACF,三角形全等的性质BE=CF;∠BAE=∠CAF可得①∠1=∠2;由ASA可得△ACN≌△ABM.④CD=DN不成立.
解:∵∠E=∠F=90°,∠B=∠C,AE=AF
∴△ABE≌△ACF
∴BE=CF
∠BAE=∠CAF
∠BAE-∠BAC=∠CAF-∠BAC
∴∠1=∠2
△ABE≌△ACF
∴∠B=∠C,AB=AC
又∠BAC=∠CAB
△ACN≌△ABM.
④CD=DN不能证明成立,3个结论对.
故答案是:①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,BE平分∠ABC,交AC边于点E,ED⊥AB,垂足为D.若△ABC的周长为12,△ADE的周长为6,则BC的长为( )

A. 3 B. 4 C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于
 AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( ) 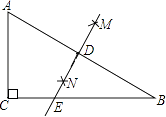
A.2
B.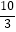
C.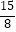
D.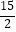
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列图案均是长度相同的火柴按一定的规律拼搭而成:第1个图案需7根火柴,第2个图案需13根火柴,…,依此规律,第11个图案需( )根火柴.
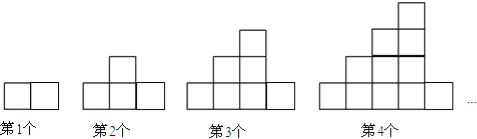
A. 156 B. 157 C. 158 D. 159
-
科目: 来源: 题型:
查看答案和解析>>【题目】将2×2的正方形网格如图所示的放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形ABCD的顶点都在格点上,若直线y=kx(k≠0)与正方形ABCD有公共点,则k不可能是( )
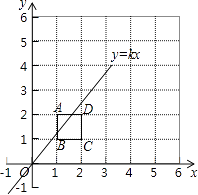
A.3
B.2
C.1
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 是等边
是等边 内一点,
内一点,  .将
.将 绕点
绕点 按顺时针方向旋转
按顺时针方向旋转 得
得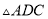 ,连接
,连接 .
.
(1)求证:
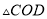 是等边三角形;
是等边三角形;(2)当
 时,试判断
时,试判断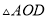 的形状,并说明理由;
的形状,并说明理由;(3)探究:当
 为多少度时,
为多少度时, 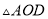 是等腰三角形?
是等腰三角形? -
科目: 来源: 题型:
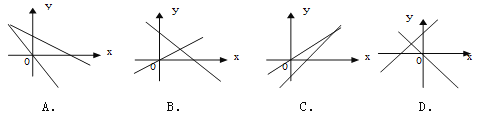
查看答案和解析>>【题目】一次函数y=kx+b与y=kbx,它们在同一坐标系内的图象可能为 ( )
相关试题

