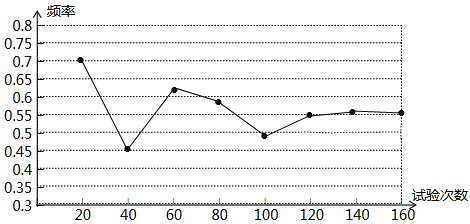
【题目】一粒木质中国象棋子“兵”,它的正面雕刻一个“兵”字,它的反面是年平的.将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下.由于棋子的两面不均匀,为了估计“兵”字面朝上的概率,某实验小组做了棋子下掷实验,实验数据如下表:
实验次数 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
“兵”字面朝上频数 | 14 | 38 | 47 | 52 | 66 | 78 | 88 | |
相应频率 | 0.7 | 0.45 | 0.63 | 0.59 | 0.52 | 0.56 | 0.55 |
(1)请将数据补充完整;
实验次数 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
“兵”字面朝上频数 | 14 | 38 | 47 | 52 | 66 | 78 | 88 | |
相应频率 | 0.7 | 0.45 | 0.63 | 0.59 | 0.52 | 0.56 | 0.55 |
(2)画出“兵”字面朝上的频率分布折线图;
(3)如果实验继续进行下去,根据上表的数据,这个实验的频率将稳定在它的概率附近,请你估计这个概率是多少?
参考答案:
【答案】
(1)18;0.55
(2)
折线图:
(3)
根据表中数据,试验频率为0.7,0.45,0.63,0.59,0.52,0.55,0.56,0.55稳定在0.55左右,故估计概率的大小为0.55.
【解析】考查利用频率估计概率,大量反复试验下频率稳定值即概率.作图时应先描点,再连线.用到的知识点为:部分的具体数目=总体数目×相应频率.频率=所求情况数与总情况数之比.(1)(3)根据图中信息,用频数除以实验次数,得到频率,由于试验次数较多,可以用频率估计概率;(2)将频率作为纵坐标,试验次数作为横坐标,描点连线,可得折线图.
【考点精析】本题主要考查了用频率估计概率的相关知识点,需要掌握在同样条件下,做大量的重复试验,利用一个随机事件发生的频率逐渐稳定到某个常数,可以估计这个事件发生的概率才能正确解答此题.
-
科目: 来源: 题型:
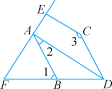
查看答案和解析>>【题目】如图,已知∠1=∠BDC,∠2+∠3=180°.
(1)请你判断DA与CE的位置关系,并说明理由;
(2)若DA平分∠BDC,CE⊥AE于E,∠1=70°,试求∠FAB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小林画出函数
 的一部分图象,利用图象回答:
的一部分图象,利用图象回答:(1)自变量x的取值范围.
(2)当x取什么值时,y的最小值.最大值各是多少?
(3)在图中,当x增大时,y的值是怎样变化?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( )
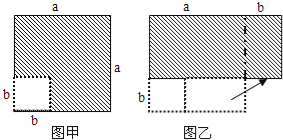
A. (a+b)2=a2+2ab+b2
B. (a﹣b)2=a2﹣2ab+b2
C. a2﹣b2=(a+b)(a﹣b)
D. (a+2b)(a﹣b)=a2+ab﹣2b2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中错误的是( ).
A.某种彩票的中奖率为1%,买100张彩票一定有1张中奖
B.从装有10个红球的袋子中,摸出1个白球是不可能事件
C.为了解一批日光灯的使用寿命,可采用抽样调查的方式
D.掷一枚普通的正六面体骰子,出现向上一面点数是2的概率是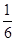
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的布袋中有分别标着数字1,2,3,4的四个乒乓球,现从袋中随机摸出两个乒乓球,则这两个乒乓球上的数字之和大于5的概率为( ).
A.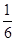
B.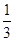
C.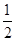
D.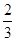
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果店以4元/千克的价格购进一批水果,由于销售状况良好,该店又再次购进同一种水果,第二次进货价格比第一次每千克便宜了0.5元,所购水果重量恰好是第一次购进水果重量的2倍,这样该水果店两次购进水果共花去了2200元.
(1)该水果店两次分别购买了多少元的水果?
(2)在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的水果有3%的损耗,第二次购进的水果有5%的损耗,该水果店希望售完这些水果获利不低于1244元,则该水果每千克售价至少为多少元?
相关试题

