【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() (x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB丄x轴于点B,点A与点B关于y轴对称.
(x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB丄x轴于点B,点A与点B关于y轴对称.

(1)求一次函数、反比例函数的解析式;
(2)求证:点C为线段AP的中点;
(3)反比例函数图象上是否存在点D,使四边形BCPD为菱形,如果存在,说明理由并求出点D的坐标;如果不存在,说明理由.
参考答案:
【答案】(1)y=![]() x+1. (2)点C为线段AP的中点. (3)存在点D,使四边形BCPD为菱形,点D(8,1)即为所求.
x+1. (2)点C为线段AP的中点. (3)存在点D,使四边形BCPD为菱形,点D(8,1)即为所求.
【解析】试题分析:(1)由点A与点B关于y轴对称,可得AO=BO,再由A的坐标求得B点的坐标,从而求得点P的坐标,将P坐标代入反比例解析式求出m的值,即可确定出反比例解析式,将A与P坐标代入一次函数解析式求出k与b的值,确定出一次函数解析式;(2)由AO=BO,PB∥CO,即可证得结论 ;(3)假设存在这样的D点,使四边形BCPD为菱形,过点C作CD平行于x轴,交PB于点E,交反比例函数y=![]() 的图象于点D,分别连结PD、BD,如图所示,即可得点D(8,1), BP⊥CD,易证PB与CD互相垂直平分,即可得四边形BCPD为菱形,从而得点D的坐标.
的图象于点D,分别连结PD、BD,如图所示,即可得点D(8,1), BP⊥CD,易证PB与CD互相垂直平分,即可得四边形BCPD为菱形,从而得点D的坐标.
试题解析:
(1)∵点A与点B关于y轴对称,
∴AO=BO,
∵A(-4,0),
∴B(4,0),
∴P(4,2),
把P(4,2)代入y=![]() 得m=8,
得m=8,
∴反比例函数的解析式:y=![]()
把A(-4,0),P(4,2)代入y=kx+b
得: ![]() ,解得:
,解得: ![]() ,
,
所以一次函数的解析式:y=![]() x+1.
x+1.
(2)∵点A与点B关于y轴对称,
∴OA=OB
∵PB丄x轴于点B,
∴∠PBA=90°,
∵∠COA=90°,
∴PB∥CO,
∴点C为线段AP的中点.
(3)存在点D,使四边形BCPD为菱形
∵点C为线段AP的中点,
∴BC= ![]() ,
,
∴BC和PC是菱形的两条边
由y=![]() x+1,可得点C(0,1),
x+1,可得点C(0,1),
过点C作CD平行于x轴,交PB于点E,交反比例函数y=![]() 的图象于点D,
的图象于点D,
分别连结PD、BD,

∴点D(8,1), BP⊥CD
∴PE=BE=1,
∴CE=DE=4,
∴PB与CD互相垂直平分,
∴四边形BCPD为菱形.
∴点D(8,1)即为所求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,对角线AC、BD交于点O,将BD绕点B逆时针旋转30°到BE所在的位置,BE与AD交于点F,分别连接DE、CE.

(1)求证:DE=DF;
(2)求证:AE∥BD;
(3)求tan∠ACE的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品进价为a元,商店将价格提高30%作零售价销售.在销售旺季过后,商店又以8折(即售价的80%)的价格开展促销活动.这时一件该商品的售价为( )
A.a元
B.0.8a元
C.1.04a元
D.0.92a元 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:M=x3﹣3xy+2x+1,N=﹣3x+xy,求多项式3M+2N,并计算当x=﹣1,y=
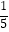 时,3M+2N的值.
时,3M+2N的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在植树节到来之际,某小区计划购进A、B两种树苗共17棵,已知A种树苗每棵80元,B种树苗每棵60元.
(1)若购进A、B两种树苗刚好用去1220元,问购进A、B两种树苗各多少棵?
(2)若购买B种树苗的数量少于A种树苗的数量,请你给出一种费用最省的方案,并求出该方案所需费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲班有54人,乙班有48人,要使甲班人数是乙班的2倍,设从乙班调往甲班人数x,可列方程( )
A.54+x=2(48﹣x)
B.48+x=2(54﹣x)
C.54﹣x=2×48
D.48+x=2×54 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( )
A. 三条直线两两相交有三个交点 B. 直线A与直线B相交于点M
C. 画一条5厘米长的线段 D. 在线段、射线、直线中直线最长
相关试题

