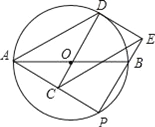
【题目】如图,AB是⊙O的直径,点P是AB下方的半圆上不与点A,B重合的一个动点,点C为AP中点,延长CO交⊙O于点D,连接AD,过点D作⊙O的切线交PB的廷长线于点E,连CE交AB于点F,连接DF.
(1)求证:△DAC≌△ECP;
(2)填空:
①四边形ACED是何种特殊的四边形?
②在点P运动过程中,线段DF、AP的数量关系是 .
参考答案:
【答案】(1)证明见解析;(2)①四边形ACED是平行四边形;②DF=![]() AP,
AP,
【解析】
(1)由已知条件易得∠CDE=∠DCA=∠DCP=∠P=90°,由此可得四边形DCPE是矩形,从而可得DC=EP,这样结合AC=PC即可由“SAS”证得△DAC≌△ECP;
(2)①由(1)中所得△DAC≌△ECP可得AD=CE,∠DAC=∠ECP,从而可得AD∥CE,由此即可得到四边形ACED是平行四边形;②由OA=OD,AD∥CE易得∠DAO=∠ADC=∠DCF,由此可得A、C、F、D四点共圆,结合∠DAF=∠ADC可得在该圆中弦DF=AC,结合点C是AP的中点即可得到DF=![]() AP.
AP.
(1)∵DE为切线,
∴OD⊥DE,
∴∠CDE=90°,
∵点C为AP的中点,
∴DC⊥AP,
∴∠DCA=∠DCP=90°,
∵AB是⊙O直径,
∴∠APB=90°,
∴四边形DEPC为矩形,
∴DC=EP,
∵在△DAC和△ECP中: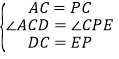 ,
,
∴△DAC≌△ECP;
(2)①∵△DAC≌△ECP,
∴AD=CE,∠DAC=∠ECP,
∴AD∥CE,
∴四边形ACED是平行四边形;
②∵OA=OD,
∴∠DAF=∠ADC,
∵AD∥CE,
∴∠ADC=∠DCF,
∴∠DAF=∠DCF,
∴A,C,F,D四点共圆,
又∵∠ADF=∠ADC,
∴AC=DF,
∵AC=![]() AP,
AP,
∴DF=![]() AP.
AP.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,直线
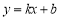 (
(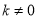 )与直线
)与直线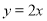 相交于点P(2,m),与x轴交于点A.
相交于点P(2,m),与x轴交于点A.
(1)求m的值;
(2)过点P作PB⊥x轴于B,如果△PAB的面积为6,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80 m,DE=10 m,求障碍物B,C两点间的距离.(结果精确到0.1 m)(参考数据:
 ≈1.414,、
≈1.414,、 ≈1.732)
≈1.732)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,OC是∠AOB的平分线.
(1)当∠AOB = 60°时,求∠AOC的度数;
(2)在(1)的条件下,过点O作OE⊥OC,补全图形,并求∠AOE的度数;
(3)当∠AOB =
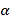 时,过点O作OE⊥OC,直接写出∠AOE的度数(用含
时,过点O作OE⊥OC,直接写出∠AOE的度数(用含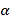 代数式表示).
代数式表示).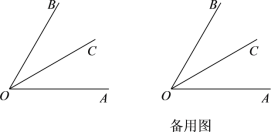
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是中国古代数学专著,在数学上有其独到的成就,不仅最早提到了分数问题,也首先记录了“盈不足”等问题.如有一道阐述“盈不足”的问题,原文如下:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?译文为:现有若干人合伙出钱买鸡,如果每人出9文钱,就会多11文钱;如果每人出6文钱,又会缺16文钱.问买鸡的人数、鸡的价格各是多少?请解答上述问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着中国经济的快速发展以及科技水平的飞速提高,中国高铁正迅速崛起.高铁大大缩短了时空距离,改变了人们的出行方式.如图,
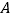 ,
,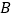 两地被大山阻隔,由
两地被大山阻隔,由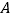 地到
地到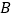 地需要绕行
地需要绕行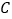 地,若打通穿山隧道,建成
地,若打通穿山隧道,建成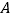 ,
,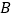 两地的直达高铁,可以缩短从
两地的直达高铁,可以缩短从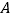 地到
地到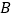 地的路程.已知:
地的路程.已知: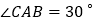 ,
,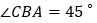 ,
,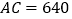 公里,求隧道打通后与打通前相比,从
公里,求隧道打通后与打通前相比,从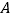 地到
地到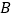 地的路程将约缩短多少公里?(参考数据:
地的路程将约缩短多少公里?(参考数据: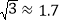 ,
,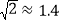 )
)
相关试题

