【题目】喜欢探究的亮亮同学拿出形状分别是长方形和正方形的两块纸片,其中长方形纸片的长为![]() ,宽为
,宽为![]() ,且两块纸片面积相等.
,且两块纸片面积相等.
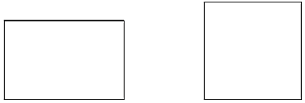
(1)亮亮想知道正方形纸片的边长,请你帮他求出正方形纸片的边长;(结果保留根号)
(2)在长方形纸片上截出两个完整的正方形纸片,面积分别为![]() 和
和![]() ,亮亮认为两个正方形纸片的面积之和小于长方形纸片的总面积,所以一定能截出符合要求的正方形纸片来,你同意亮亮的见解吗?为什么?(参考数据:
,亮亮认为两个正方形纸片的面积之和小于长方形纸片的总面积,所以一定能截出符合要求的正方形纸片来,你同意亮亮的见解吗?为什么?(参考数据:![]() ,
,![]() )
)
参考答案:
【答案】(1)![]() ;(2)不同意,理由见解析
;(2)不同意,理由见解析
【解析】
(1)设正方形边长为![]() ,根据两块纸片面积相等列出方程,再根据算术平方根的意义即可求出x的值;
,根据两块纸片面积相等列出方程,再根据算术平方根的意义即可求出x的值;
(2)根据两个正方形纸片的面积计算出两个正方形的边长,计算两个正方形边长的和,并与3比较即可解答.
解:(1)设正方形边长为![]() ,则
,则![]() ,由算术平方根的意义可知
,由算术平方根的意义可知![]() ,
,
所以正方形的边长是![]() .
.
(2)不同意.
因为:两个小正方形的面积分别为![]() 和
和![]() ,则它们的边长分别为
,则它们的边长分别为![]() 和
和![]() .
.![]() ,即两个正方形边长的和约为
,即两个正方形边长的和约为![]() ,
,
所以![]() ,即两个正方形边长的和大于长方形的长,
,即两个正方形边长的和大于长方形的长,
所以不能在长方形纸片上截出两个完整的面积分别为![]() 和
和![]() 的正方形纸片.
的正方形纸片.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线AB∥DF,∠D+∠B=180°,

(1)求证:DE∥BC;
(2)如果∠AMD=75°,求∠AGC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线AB与直线CD相交于点O,OE平分
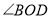 .
.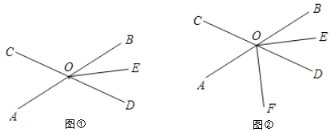
(1)如图①,若
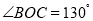 ,求
,求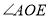 的度数;
的度数;(2)如图②,射线OF在
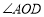 内部.
内部.①若
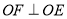 ,判断OF是否为
,判断OF是否为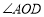 的平分线,并说明理由;
的平分线,并说明理由;②若OF平分
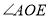 ,
,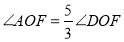 ,求
,求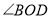 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这
个分式为“和谐分式”.
(1)下列分式:①
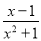 ;②
;②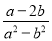 ;③
;③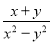 ;④
;④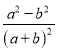 . 其中是“和谐分式”是 (填写序号即可);
. 其中是“和谐分式”是 (填写序号即可);(2)若
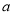 为正整数,且
为正整数,且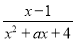 为“和谐分式”,请写出
为“和谐分式”,请写出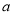 的值;
的值;(3)在化简
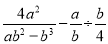 时,
时,小东和小强分别进行了如下三步变形:
小东:
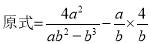
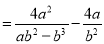
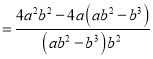
小强:
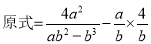
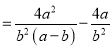
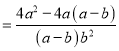
显然,小强利用了其中的和谐分式, 第三步所得结果比小东的结果简单,
原因是: ,
请你接着小强的方法完成化简.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在
 中,
中,  .
.(1)求作:
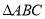 的角平分线
的角平分线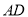 (要求:尺规作图,不写作法,保留作图痕迹);
(要求:尺规作图,不写作法,保留作图痕迹); (2)在(1)的条件下,若
 ,
,  ,求
,求 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
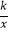 (x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
(x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )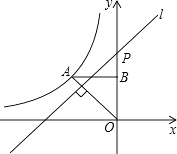
A.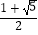
B.
C.
D.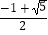
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,以△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,试判断△ABC与△AEG面积之间的关系,并说明理由。

(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地多少平方米?

相关试题

