【题目】如图:

(1)如图1,将长方形纸片ABFE沿着线段DC折叠,CF交AD于点H,过点H作HG∥DC,交线段CB于点G.
①判断∠FHG与∠EDC是否相等,并说明理由;
②说明HG平分∠AHC的理由.
(2)如图2,如果将(1)中的已知条件改为折叠三角形纸片ABE,其它条件不变.HG是否平分∠AHC?如果平分请说明理由;如果不平分,请找出∠CHG,∠AHG与∠E的数量关系并说明理由.
参考答案:
【答案】(1)①∠FHG=∠EDC,见解析;②见解析;(2)HG不再平分∠AHC,∠AHG=∠CHG+∠E,见解析.
【解析】
(1) ①根据平行线性质得∠EDA=∠FHA,∠ADC=∠AHG,由角的计算即可得证.
② HG平分∠AHC,理由如下:将图形折回到其原始状态,E的对应点为N,F的对应点为M,由折叠性质知:∠FCD=∠DCM,根据平行线性质得:∠DCM=∠HGC,∠DCH=∠CHG,∠CGH=∠AHG,等量代换得∠CHG=∠AHG,根据角平分线定义即可得证.
(2) HG不再平分∠AHC,∠AHG=∠CHG+∠E;理由如下:如图:延长线段AD和BC交于点F,根据平行线性质得:∠CHG=∠DCH=∠FCD,∠AHG=∠ADC,由三角形内角和定理、等量代换即可得证.
(1)①如图1,
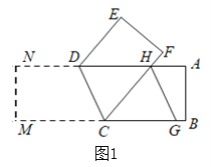
∵DE∥CF,
∴∠EDA=∠FHA(两直线平行,同位角相等),
∵HG∥DC,
∠ADC=∠AHG(两直线平行,同位角相等),
∴∠EDA +∠ADC=∠FHA +∠AHG,
∴∠FHG=∠EDC.
② HG平分∠AHC,理由如下:
将图形折回到其原始状态,E的对应点为N,F的对应点为M,
由折叠知∠FCD=∠DCM.
∵HG∥DC,
∴∠DCM=∠HGC(两直线平行,同位角相等),
∠DCH=∠CHG(两直线平行,内错角相等),
∵AD∥BC,
∴∠CGH=∠AHG(两直线平行,内错角相等),
∴∠CHG=∠AHG,
即HG平分∠AHC.
(2)HG不再平分∠AHC.∠AHG=∠CHG+∠E.
理由如下:
如图2,延长线段AD和BC交于点F,
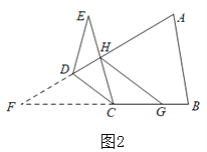
得到∠ECD=∠FCD.
∵HG∥DC,
∴∠CHG=∠DCH=∠FCD,
∠AHG=∠ADC,
∵∠ADC+∠FDC=180
又∵∠F+∠FCD+∠FDC=180
∴∠AHG=∠CHG+∠E
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个长方形的长和宽分别为x厘米和y厘米(x,y为正整数),如果将长方形的长和宽各增加5厘米得到新的长方形,面积记为
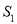 ,将长方形的长和宽各减少2厘米得到新的长方形,面积记为
,将长方形的长和宽各减少2厘米得到新的长方形,面积记为 .
.(1)请说明:
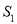 与
与 的差一定是7的倍数.
的差一定是7的倍数.(2)如果
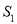 比
比 大196
大196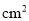 ,求原长方形的周长.
,求原长方形的周长.(3)如果一个面积为
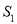 的长方形和原长方形能够没有缝隙没有重叠的拼成一个新的长方形,请找出x与y的关系,并说明理由.
的长方形和原长方形能够没有缝隙没有重叠的拼成一个新的长方形,请找出x与y的关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】重庆实验外国语学校是一所外语小班制教学的特色学校,初二年级某英语小班共有
 名同学,学号依次为
名同学,学号依次为 号,
号, 号,……20号,现随机分成甲、乙、丙三个小组,每组人数若干.若将乙组的小东(
号,……20号,现随机分成甲、乙、丙三个小组,每组人数若干.若将乙组的小东( 号)调整到甲组,将丙组的小英(
号)调整到甲组,将丙组的小英( 号)调整到乙组,此时甲、丙两组同学学号的平均数都将比调整前增加
号)调整到乙组,此时甲、丙两组同学学号的平均数都将比调整前增加 ,乙组同学学号的平均数将比调整前增加
,乙组同学学号的平均数将比调整前增加 ;同时乙组的小强(
;同时乙组的小强( 号)经过计算发现,他的学号数高于调整前乙组同学学号的平均数,却低于调整后乙组的平均数则调整前甲组共有_____名同学.
号)经过计算发现,他的学号数高于调整前乙组同学学号的平均数,却低于调整后乙组的平均数则调整前甲组共有_____名同学. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进一批日用品,若按每件5元的价格销售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件,假定每月销售件数
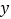 (件)与价格
(件)与价格  (元/件)之间满足一次函数关系.
(元/件)之间满足一次函数关系.
(1)试求:y与x之间的函数关系式;
(2)这批日用品购进时进价为4元,则当销售价格定为多少时,才能使每月的润最大?每月的最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人同时登西山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图11所示,乙在A处提速后的速度是甲登山速度的3.根据图象所提供的信息解答下列问题中正确的个数为( )

(1)甲登山的速度是每分钟10米.
(2)乙在A地提速时距地面的高度b为30米.
(3)登山9分钟时,乙追上了甲.
(4)乙在距地面的高度为165米时追上甲.
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】盒子里装有12张红色卡片,16张黄色卡片,4张黑色卡片和若干张蓝色卡片,每张卡片除颜色外都相同,从中任意摸出一张卡片,摸到红色卡片的概率是0.24.
(1)从中任意摸出一张卡片,摸到黑色卡片的概率是多少?
(2)求盒子里蓝色卡片的个数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 与
与  轴、
轴、  轴分别相交于点A(-1,0)和B(0,3),其顶点为D.
轴分别相交于点A(-1,0)和B(0,3),其顶点为D.
(1)求这条抛物线的解析式;
(2)若抛物线与 轴的另一个交点为E,求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短.若存在请求出点P的坐标,若不存在说明理由.
轴的另一个交点为E,求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短.若存在请求出点P的坐标,若不存在说明理由.
相关试题

