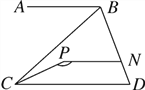
【题目】如图,已知AB∥PN∥CD.
(1)试探索∠ABC,∠BCP和∠CPN之间的数量关系,并说明理由;
(2)若∠ABC=42°,∠CPN=155°,求∠BCP的度数.
参考答案:
【答案】(1)见解析;(2)17°
【解析】试题分析:(1)由平行线的性质得出∠ABC=∠BMN=∠BCD,∠CPN+∠PCD=180°,即可得出结论;
(2)由(1)的结论代入计算即可.
试题解析:(1)∠ABC-∠BCP+∠CPN=180°;理由如下:
延长NP交BC于M,如图所示:
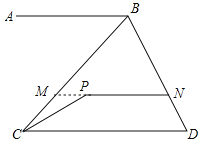
∵AB∥PN∥CD,
∴∠ABC=∠BMN=∠BCD,∠CPN+∠PCD=180°,
∵∠PCD=∠BCD-∠BCP=∠ABC-∠BCP,
∴∠ABC-∠BCP+∠CPN=180°.
(2)由(1)得:∠ABC-∠BCP+∠CPN=180°,
则∠BCP=∠ABC+∠CPN-180°=155°+42°-180°=17°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】推理填空:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
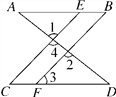
∵∠1=∠2(已知),且∠1=∠4(____________),
∴∠2=∠4(等量代换),
∴CE∥BF(__________________________),
∴∠________=∠3(______________________).
又∵∠B=∠C(已知),
∴∠3=∠B(等量代换).
∴AB∥CD(__________________________).
-
科目: 来源: 题型:
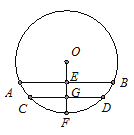
查看答案和解析>>【题目】如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深GF=2cm.若水面上升2cm(EG=2cm),则此时水面宽
AB为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x、y的方程组
 .
.(1)当a满足22a+3﹣22a+1=96时,求方程组的解;
(2)当程组的解满足x+y=16时,求a的值;
(3)试说明:不论a取什么实数,x的值始终为正数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:求l+2+22+23+24+…+22013的值.
解:设S=l+2+22+23+24+…+22012+22013,将等式两边同时乘2,
得2S=2+22+23+24+25+…+22013+22014. 将下式减去上式,得2S﹣S=22014-1
即S=22014-1,
即1+2+22+23+24+…+22013=22014-1
仿照此法计算:(1)1+3+32+33+…+3100;(2)1+
 +
+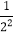 +
+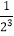 +…+
+…+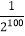 ,
, -
科目: 来源: 题型:
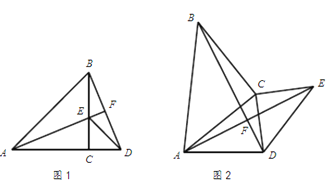
查看答案和解析>>【题目】在△ABC和△DEC中,AC=BC,DC=EC,∠ACB=∠ECD=90°.
(1)如图1,当点A、C、D在同一条直线上时,AC=12,EC=5,
①求证:AF⊥BD; ②求AF的长度;
(2)如图2,当点A、C、D不在同一条直线上时,求证:AF⊥BD.
相关试题

