【题目】如图,MN是⊙O的直径,QN是⊙O的切线,连接MQ交⊙O于点H,E为![]() 上一点,连接ME,NE,NE交MQ于点F,且ME2=EFEN.
上一点,连接ME,NE,NE交MQ于点F,且ME2=EFEN.
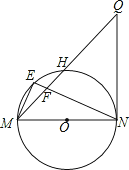
(1)求证:QN=QF;
(2)若点E到弦MH的距离为1,cos∠Q=![]() ,求⊙O的半径.
,求⊙O的半径.
参考答案:
【答案】(1)证明见解析;(2)2.5.
【解析】
试题分析:(1)如图1,通过相似三角形(△MEF∽△MEN)的对应角相等推知,∠1=∠EMN;又由弦切角定理、对顶角相等证得∠2=∠3;最后根据等角对等边证得结论;
(2)如图2,连接OE交MQ于点G,设⊙O的半径是r.根据(1)中的相似三角形的性质证得∠EMF=∠ENM,所以由“圆周角、弧、弦间的关系”推知点E是弧MH的中点,则OE⊥MQ;然后通过解直角△MNE求得cos∠Q=sin∠GMO=![]() ,则可以求r的值.
,则可以求r的值.
试题解析:(1)如图1,
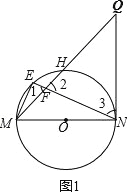
∵ME2=EFEN,
∴![]() .
.
又∵∠MEF=∠MEN,
∴△MEF∽△MEN,
∴∠1=∠EMN.
∵∠1=∠2,∠3=∠EMN,
∴∠2=∠3,
∴QN=QF;
(2)解:如图2,连接OE交MQ于点G,设⊙O的半径是r.
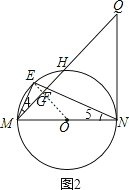
由(1)知,△MEF∽△MEN,则∠4=∠5.
∴![]() .
.
∴OE⊥MQ,
∴EG=1.
∵cos∠Q=![]() ,且∠Q+∠GMO=90°,
,且∠Q+∠GMO=90°,
∴sin∠GMO=![]() ,
,
∴![]() ,即
,即![]() ,
,
解得,r=2.5,即⊙O的半径是2.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣2a3)2的结果是( )
A. 2a5 B. 4a5 C. ﹣2a6 D. 4a6
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知(x2+px+8)(x2-3x+q)的展开式中不含x2和x3项,求p,q的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.
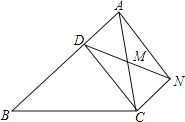
①求证:CD=AN;
②若∠AMD=2∠MCD,求证:四边形ADCN是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】4的平方根为_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运动属于平移的是( )
A. 荡秋千
B. 推开教室的门
C. 风筝在空中随风飘动
D. 急刹车时,汽车在地面上的滑动
-
科目: 来源: 题型:
查看答案和解析>>【题目】若代数式2y2+3y+7的值为8,那么4y2+6y﹣9的值为( )
A.2 B.﹣17 C.﹣7 D.7
相关试题

