【题目】若关于x的方程x2-(k+3)x+3k=0的两根之差为8,则k的值为___.
参考答案:
【答案】-5或11
【解析】
由根与系数的关系可知:x1+x2=k+3,x1x2=3k;又知两根之差为8,即|x1-x2|=8,根据(x1-x2)2=(x1+x2)2-4x1x2,建立等量关系求k.
由根与系数的关系可知:x1+x2=k+3,x1x2=3k.
由已知两根之差为8,得|x1-x2|=8,即(x1-x2)2=64.
则(x1+x2)2-4x1x2=64,
(k+3)2-4×3k=64,
解得k=11或-5.
故答案为:11或-5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式2x2+bx+c分解因式为2(x﹣3)(x+1),则b、c的值为( )
A.b=3,c=﹣1
B.b=﹣6,c=2
C.b=﹣6,c=﹣4
D.b=﹣4,c=﹣6 -
科目: 来源: 题型:
查看答案和解析>>【题目】命题“相等的角是对顶角”是命题(填“真”或“假”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在同一平面内,将△ABC绕点A旋转到△AED的位置,若AE⊥BC,∠ADC=65°,则∠ABC的度数为( )

A.30°
B.40°
C.50°
D.60° -
科目: 来源: 题型:
查看答案和解析>>【题目】一个直角三角形三边的长为一组连续自然数,求该直角三角形的三边长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,三角形ABC的顶点都在网格点上.
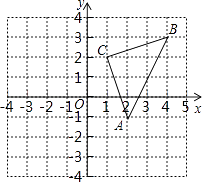
(1)平移三角形ABC,使点C与坐标原点O是对应点,请画出平移后的三角形A′B′C′;
(2)写出A,B两点的对应点A′,B′的坐标;
(3)请直接写出三角形ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】将△ABC绕O点顺时针旋转50°得△A1B1C1(A、B分别对应A1、B1),则直线AB与直线A1B1的夹角(锐角)为( )
A.130°
B.50°
C.40°
D.60°
相关试题

