搜索
【题目】计算：
（1）
；
（2）m2m4+（﹣m3）2；
（3）（x+y）（2x﹣3y）；
（4）（x+3）2﹣（x+1）（x﹣1）．
参考答案：
【答案】（1）
；（2）2m6；（3）2x2﹣xy﹣3y2；（4）6x+10．
【解析】
（1）根据同底数幂的乘法法则进行计算；
（2）先根据同底数幂的乘法法则和幂的乘方法则进行计算，再根据合并同类项法则进行计算；
（3）根据多项式乘以多项式法则进行计算，再合并同类项；
（4）先根据完全平方公式，平方差公式进行计算，再合并同类项．
解：（1）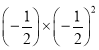
＝
；
（2）m2m4+（﹣m3）2
＝m6+m6
＝2m6；
（3）（x+y）（2x﹣3y）
＝2x2﹣3xy+2xy﹣3y2
＝2x2﹣xy﹣3y2；
（4）（x+3）2﹣（x+1）（x﹣1）
＝x2+6x+9﹣x2+1
＝6x+10．
-
科目： 来源： 题型：
查看答案和解析>>【题目】复杂的数学问题我们常会把它分解为基本问题来研究，化繁为简，化整为零这是一种常见的数学解题思想．
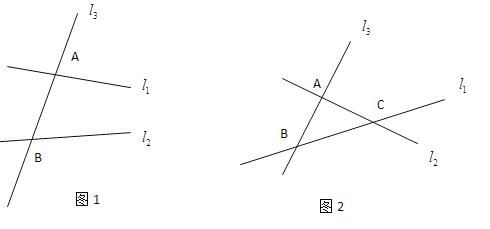
（1）如图1，直线
，
被直线
所截，在这个基本图形中，形成了______对同旁内角．（2）如图2，平面内三条直线
，，两两相交，交点分别为
、
、
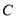，图中一共有______对同旁内角．（3）平面内四条直线两两相交，最多可以形成______对同旁内角．
（4）平面内
条直线两两相交，最多可以形成______对同旁内角． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，E、F分别是正方形ABCD的边CD、AD上的点，且CE＝DF，AE、BF相交于点O，下列结论①AE＝BF；②AE⊥BF；③AO＝OE；④S△AOB＝S四边形DEOF中，错误的有（ ）
A.1个B.2个C.3个D.4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）问题发现：如图 1，已知点 F，G 分别在直线 AB，CD 上，且 AB∥CD，若∠BFE=40°，∠CGE=130°，则∠GEF 的度数为 ；
（2）拓展探究：∠GEF，∠BFE，∠CGE 之间有怎样的数量关系？写出结论并给出证明； 答：∠GEF= .
证明：过点 E 作 EH∥AB，
∴∠FEH=∠BFE（ ），
∵AB∥CD，EH∥AB，（辅助线的作法）
∴EH∥CD（ ），
∴∠HEG=180°-∠CGE（ ），
∴∠FEG=∠HFG+∠FEH= .
（3）深入探究：如图 2，∠BFE 的平分线 FQ 所在直线与∠CGE 的平分线相交于点 P，试探究∠GPQ 与∠GEF 之间的数量关系，请直接写出你的结论．
-
科目： 来源： 题型：
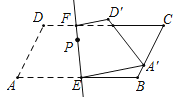
查看答案和解析>>【题目】如图，直线EF分别交平行四边形ABCD边AB、CD于直E、F，将图形沿直线EF对折，点A、D分別落在点A′、D′处．若∠A=60°，AD=4，AB=8，当点A′落在BC边上任意点时，设点P为直线EF上的动点，请直接写出PC+PA′的最小值（ ）
A.4+
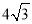B.8C.6+
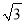D.4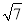
-
科目： 来源： 题型：
查看答案和解析>>【题目】在矩形ABCD中，AD=5，AB=4，点E，F在直线AD上，且四边形BCFE为菱形，若线段EF的中点为点M，则线段AM的长为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料：
求1+2+22+23+24+…+22020的值．
解：设S＝1+2+22+23+24+…+22020，将等式两边同时乘以2得，
2S＝2+22+23+24+25+…+22021．
将下式减去上式，得2S﹣S＝22021﹣1，即S＝22021﹣1．
即1+2+22+23+24+…+22020＝22021﹣1
仿照此法计算：
（1）1+3+32+33+…+320；
（2）
．
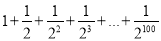相关试题
