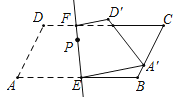
【题目】如图,直线EF分别交平行四边形ABCD边AB、CD于直E、F,将图形沿直线EF对折,点A、D分別落在点A′、D′处.若∠A=60°,AD=4,AB=8,当点A′落在BC边上任意点时,设点P为直线EF上的动点,请直接写出PC+PA′的最小值( )
A.4+![]() B.8C.6+
B.8C.6+![]() D.4
D.4![]()
参考答案:
【答案】D
【解析】
连接AC交EF于P′,连接P′A′,作CH⊥AB交AB的延长线于H.因为A、A′关于直线EF对称,推出P′A′=P′A,推出P′A′+P′C=P′A+P′C=AC,推出当点P与P′重合时,PA′+PC的值最小,最小值=AC的长;
如图,连接AC交EF于P′,连接P′A′,作CH⊥AB交AB的延长线于H.
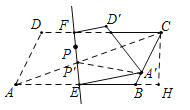
∵A、A′关于直线EF对称,
∴P′A′=P′A,
∴P′A′+P′C=P′A+P′C=AC,
∴当点P与P′重合时,PA′+PC的值最小,最小值=AC的长.
在Rt△BCH中,∵BC=4,∠CBH=60°,
∴BH=2,CH=2![]() ,
,
∴AH=AB+BH=10,
在Rt△ACH中,AC=![]() .
.
∴PC+PA′的最小值为![]() ,
,
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,错误的有( )

A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题发现:如图 1,已知点 F,G 分别在直线 AB,CD 上,且 AB∥CD,若∠BFE=40°,∠CGE=130°,则∠GEF 的度数为 ;

(2)拓展探究:∠GEF,∠BFE,∠CGE 之间有怎样的数量关系?写出结论并给出证明; 答:∠GEF= .
证明:过点 E 作 EH∥AB,

∴∠FEH=∠BFE( ),
∵AB∥CD,EH∥AB,(辅助线的作法)
∴EH∥CD( ),
∴∠HEG=180°-∠CGE( ),
∴∠FEG=∠HFG+∠FEH= .
(3)深入探究:如图 2,∠BFE 的平分线 FQ 所在直线与∠CGE 的平分线相交于点 P,试探究∠GPQ 与∠GEF 之间的数量关系,请直接写出你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
 ;
;(2)m2m4+(﹣m3)2;
(3)(x+y)(2x﹣3y);
(4)(x+3)2﹣(x+1)(x﹣1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AD=5,AB=4,点E,F在直线AD上,且四边形BCFE为菱形,若线段EF的中点为点M,则线段AM的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
求1+2+22+23+24+…+22020的值.
解:设S=1+2+22+23+24+…+22020,将等式两边同时乘以2得,
2S=2+22+23+24+25+…+22021.
将下式减去上式,得2S﹣S=22021﹣1,即S=22021﹣1.
即1+2+22+23+24+…+22020=22021﹣1
仿照此法计算:
(1)1+3+32+33+…+320;
(2)
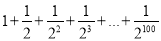 .
. -
科目: 来源: 题型:
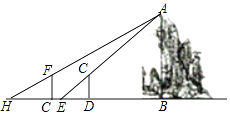
查看答案和解析>>【题目】假山具有多方面的造景功能,与建筑、植物等组合成富于变化的景致.某公园有一座假山,小亮、小慧等同学想用一些测量工具和所学的几何知识测量这座假山的高度来检验自己掌握知识和运用知识的能力,如图,在阳光下,小亮站在水平地面的D处,此时小亮身高的影子顶端与假山的影子顶端E重合,这时小亮身高CD的影长DE=2米,一段时间后,小亮从D点沿BD的方向走了3.6米到达G处,此时小亮身高的影子顶端与假山的影子顶端H重合,这时小亮身高的影长GH=2.4米,已知小亮的身高CD=FG=1.5米,点G,E,D均在直线BH上,AB⊥BH,CD⊥BH,GF⊥BH,请你根据题中提供的相关信息,求出假山的高度AB.
相关试题

