搜索
【题目】若关于x的方程x2+2x﹣a=0有两个相等的实数根，则a的值为（ ）
A.﹣1
B.1
C.﹣4
D.4
参考答案：
【答案】A
【解析】解：∵方程x2+2x﹣a=0有两个相等的实数根， ∴△=22﹣4×1×（﹣a）=4+4a=0，
解得：a=﹣1．
故选A．
根据方程的系数结合根的判别式可得出关于a的一元一次方程，解方程即可得出结论．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校举行了“文明在我身边”摄影比赛.已知每幅参赛作品成绩记为
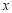分(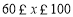
).校方从600幅参赛作品中随机抽取了部分参赛作品，统计了它们的成绩，并绘制了如下不完整的统计图表.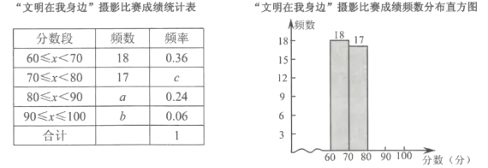
根据以上信息解答下列问题：
(1)统计表中
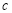的值为 ；样本成绩的中位数落在分数段 中；(2)补全频数分布直方图；
(3)若80分以上(含80分)的作品将被组织展评，试估计全校被展评作品数量是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知(m-2)x|m-1|+y=0是关于x，y的二元一次方程，则m=______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】综合题。
（1）计算：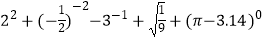
（2）解方程：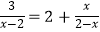
-
科目： 来源： 题型：
查看答案和解析>>【题目】BM是△ABC中AC边上的中线，AB=5cm，BC=3cm，那么△ABM与△BCM的周长之差为___cm．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图示，若△ABC内一点P满足∠PAC=∠PBA=∠PCB，则点P为△ABC的布洛卡点．三角形的布洛卡点（Brocard point）是法国数学家和数学教育家克洛尔（A．L．Crelle 1780﹣1855）于1816年首次发现，但他的发现并未被当时的人们所注意，1875年，布洛卡点被一个数学爱好者法国军官布洛卡（Brocard 1845﹣1922）重新发现，并用他的名字命名．问题：已知在等腰直角三角形DEF中，∠EDF=90°，若点Q为△DEF的布洛卡点，DQ=1，则EQ+FQ=（ ）
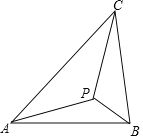
A．5 B．4 C．3+
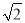D．2+ -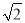
科目： 来源： 题型：
查看答案和解析>>【题目】锐角三角形的三条高都在______，钝角三角形有_____条高在三角形外，直角三角形有两条高恰是它的______．
相关试题
