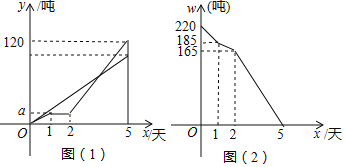
【题目】某市制米厂接到加工大米任务,要求5天内加工完220吨大米,制米厂安排甲、乙两车间共同完成加工任务,乙车间加工中途停工一段时间维修设备,然后改变加工效率继续加工,直到与甲车间同时完成加工任务为止.设甲、乙两车间各自加工大米数量y(吨)与甲车间加工时间s(天)之间的关系如图(1)所示;未加工大米w(吨)与甲加工时间x(天)之间的关系如图(2)所示,请结合图象回答下列问题:
(1)甲车间每天加工大米 吨,a= .
(2)求乙车间维修设备后,乙车间加工大米数量y(吨)与x(天)之间函数关系式.
(3)若55吨大米恰好装满一节车厢,那么加工多长时间装满第一节车厢?再加工多长时间恰好装满第二节车厢?
参考答案:
【答案】(1)20,15;(2)y=35x﹣55;(3)再过1天装满第二节车厢.
【解析】(1)根据题意,由图2得出两个车间同时加工和甲单独加工的速度;
(2)用待定系数法解决问题;
(3)求出两个车间每天加工速度分别计算两个55吨完成的时间.
(1)由图象可知,第一天甲乙共加工220﹣185=35吨,
第二天,乙停止工作,甲单独加工185﹣165=20吨,
则乙一天加工35﹣20=15吨,a=15,
故答案为:20,15;
(2)设y=kx+b,
把(2,15),(5,120)代入得![]() ,
,
解得:![]() ,
,
∴y=35x﹣55(2≤x≤5);
(3)①当0<x≤1时,20+15=35<55,不合理,
②当1<x≤2是地,20x+15=55,x=2,
③当2<x≤5时,20x+35x-55=110,x=3,
3-2=1(天),
所以生产2天可装满第一节车厢,再经过1天可装满第二节车厢.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:x1,x2,…x2012都是不等于0的有理数,请你探究以下问题:
(1)若y1=
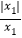 ,则
,则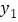 = ;
= ;(2)若y2=
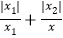 ,则
,则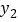 = ;
= ;(3)若y3=
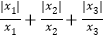 ,则
,则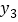 = ;
= ;(4)由以上探究可知,y2012=
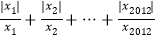 ,
,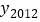 共有 个不同的值。请求出这些不同的y2012的值的绝对值的和。
共有 个不同的值。请求出这些不同的y2012的值的绝对值的和。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:b是最小的正整数,且a、b满足
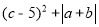 =0,请回答问题
=0,请回答问题(1)请直接写出a、b、c的值。
a=__________; b=__________;c=__________
(2)a、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在0到2之间运动时(即0≤x≤2时),请化简式子:
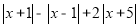 (请写出化简过程)
(请写出化简过程)
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB。请问:BC-AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】李军同学早晨起来跑步,他从自家向东跑了2千米到达谢彬家,继续向东跑了1.5千米到达红红家,然后向西跑了4.5千米到达了学校,最后回到家.请按要求完成下列各题.
(1)以李军家为原点,以向东的方向为正方向,用1个单位长度表示1千米,请你画出数轴,并在数轴上表示出李军、谢彬、红红家及学校的位置及各位置表示的有理数;
(2)谢彬家距学校多远?
(3)李军一共跑了多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某一食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:

这批样品的平均质量比标准质量多还是少?多或少几克,若标准质量为450克,则抽样检测的总质量是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于气温,有的地方用摄氏温度表示,有的地方用华氏温度表示,摄氏温度与华氏温度之间存在一次函数关系.从温度计的刻度上可以看出,摄氏温度x(℃)与华氏温度y(℉)有如下的对应关系:
x(℃)
…
-10
0
10
20
30
…
y(℉)
…
14
32
50
68
86
…
(1)试确定y与x之间的函数关系。
(2)某天,滨海的最高气温是25℃,澳大利亚悉尼的最高气温80℉,这一天哪个地区的最高气温较高?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两同学在一次百米赛跑中,路程S(米)与时间t(秒)之间的关系如图所示.根据图象回答下列问题:

(1)3.8秒时,哪位同学处于领先位置?
(2)在这次赛跑中,哪位同学先到达终点?比另一个同学早多少时间到达?约几秒后哪位同学被哪位同学追上?
(3)甲同学所走的路程S(米)与时间t(秒)之间的函数关系式.
相关试题

