【题目】近年来,随着社会竞争的日益激烈,家长为使孩子不输在教育的起跑线上,不惜花费重金购置教育质量好的学区的房产.张先生准备购买一套小户型学区房,他去某楼盘了解情况得知,该户型的单价是12000元/m2 , 面积如图所示(单位:米,卫生间的宽未定,设宽为x米),售房部为张先生提供了以下两种优惠方案: 方案一:整套房的单价是12000元/m2 , 其中厨房可免费赠送 ![]() 的面积;
的面积;
方案二:整套房按原销售总金额的9折出售.
(1)用y1表示方案一中购买一套该户型商品房的总金额,用y2表示方案二中购买一套该户型商品房的总金额,分别求出两种方案中的总金额y1、y2(用含x的式子表示);
(2)求当x=2时,两种方案的总金额分别是多少元?
(3)张先生因现金不够,在银行借了18万元住房贷款,贷款期限为6年,从开始贷款的下一个月起逐月偿还,贷款月利率是0.5%,每月还款数额=平均每月应还的贷款本金数额+月利息,月利息=上月所剩贷款本金数额×月利率. ①张先生借款后第一个月应还款数额是多少元?
②假设贷款月利率不变,若张先生在借款后第n(1≤n≤72,n是正整数)个月的还款数额为P,请写出P与n之间的关系式.
参考答案:
【答案】
(1)解:y1=12000×(18+12+6× ![]() +2x)=12000×(2x+32)=24000x+384000,
+2x)=12000×(2x+32)=24000x+384000,
y2=12000×(18+12+6+2x)×0.9=12000×(2x+36)×0.9=21600x+388800
(2)解:当x=2时,y1=2400×2+384000=432000(元);
y2=21600×2+388800=432000(元);
故当x=2时,两种方案的金额均为432000元
(3)解:①180000÷(12×6)=2500(元)2500+180000×0.5%=3400(元)
答:张先生借款后第一个月应还3400元.
②P=2500+[180000﹣2500(n﹣1)]×0.5%=﹣12.5n+3412.5
【解析】(1)根据图中线段长度,即可表示出各部分面积,进而得出两种购买方案;(2)利用两关系式直接得出答案;(3)①根据贷款数以及利率即可得出张先生借款后第一个月应还款数额;②可以得出还款数额为2500+[180000﹣(n﹣1)×2500]×0.5%,进而得出即可.
-
科目: 来源: 题型:
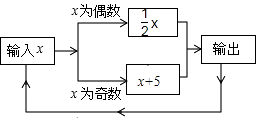
查看答案和解析>>【题目】下面有一数值转换器,原理如图所示,若开始输入的x的值是22,则第1次输出的结果是11,第2次输出的结果是16,依次继续下去,则第2015次输出的结果是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入表示它所在的集合里.
﹣2,7,﹣1.732,0,3.14,﹣(+5),﹣ ,﹣(﹣3),2007
,﹣(﹣3),2007
(1)正数集合{ …}
(2)负数集合{ …}
(3)整数集合{ …}
(4)有理数集合{ …}. -
科目: 来源: 题型:
查看答案和解析>>【题目】“低碳生活,绿色出行”,自行车正逐渐成为人们喜爱的交通工具.某运动商城的自行车销售量自2017年起逐月增加,据统计,该商城1月份销售自行车64辆,3月份销售了100辆.
(1)若该商城前4个月的自行车销量的月平均增长率相同,问该商城4月份卖出多少辆自行车?
(2)考虑到自行车需求不断增加,该商城准备投入3万元再购进一批两种规格的自行车,已知A型车的进价为500元/辆,售价为700元/辆,B型车进价为1000元/辆,售价为1300元/辆.根据销售经验,A型车不少于B型车的2倍,但不超过B型车的2.8倍.假设所进车辆全部售完,为使利润最大,该商城应如何进货?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD中,AC与BD交于点O,如果只给出条件“AB∥CD”,那么可以判定四边形ABCD是平行四边形的是( ) ①再加上条件“BC=AD”,则四边形ABCD一定是平行四边形.
②再加上条件“∠BAD=∠BCD”,则四边形ABCD一定是平行四边形.
③再加上条件“AO=CO”,则四边形ABCD一定是平行四边形.
④再加上条件“∠DBA=∠CAB”,则四边形ABCD一定是平行四边形.
A.①和②
B.①③和④
C.②和③
D.②③和④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某大楼的顶部有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1∶
 ,AB=10米,AE=15米(i=1∶
,AB=10米,AE=15米(i=1∶ 是指坡面的铅直高度BH与水平长度AH的比).
是指坡面的铅直高度BH与水平长度AH的比).
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:
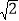 ≈1.414,
≈1.414, ≈1.732)
≈1.732) -
科目: 来源: 题型:
查看答案和解析>>【题目】某种出租车的收费标准:起步价7元(即行驶距离不超过3千米都需付7元车费),超过3千米后,每增加1千米,加收2.4元(不足1千米按1千米计).某人乘这种出租车从甲地到乙地共付车费19元,那么甲地到乙地路程的最大值是( )
A.5千米
B.7千米
C.8千米
D.15千米
相关试题

