【题目】如图,E,F是四边形ABCD对角线AC上的两点,AD∥BC,DF∥BE,AE=CF.
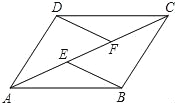
求证:(1)△AFD≌△CEB;(2)四边形ABCD是平行四边形.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)根据全等三角形的判定定理ASA证得△AFD≌△CEB;
(2)利用(1)中的全等三角形的对应边相等得到AD=CB,则由“有一组对边相等且平行的四边形是平行四边形”证得结论.
试题解析:(1)如图,∵AD∥BC,DF∥BE,
∴∠1=∠2,∠3=∠4.
又AE=CF,
∴AE+EF=CF+EF,即AF=CE.
在△AFD与△CEB中,
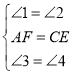 ,
,
∴△AFD≌△CEB(ASA);
(2)由(1)知,△AFD≌△CEB,则AD=CB.
又∵AD∥BC,
∴四边形ABCD是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解方程
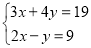
(2)计算:
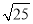 +
+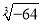 —
—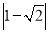
(3) 解方程 (2x-1)2=36
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中:①∠A+∠B=∠C;②∠A﹕∠B﹕∠C=1﹕2﹕3;③∠A=
 ∠B=
∠B= ∠C;④∠A=∠B=2∠C;⑤∠A=∠B=
∠C;④∠A=∠B=2∠C;⑤∠A=∠B= ∠C,能确定△ABC为直角三角形的条件有( )
∠C,能确定△ABC为直角三角形的条件有( )A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)
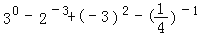
(2)(﹣2x2)3+x2x4﹣(﹣3x3)2
(3)(x+2)2﹣(x+1)(x﹣1)
(4)(﹣2a﹣b+3)(﹣2a+b+3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列从左到右的变形,是因式分解的是( )
A. (3-x)(3+x)=9-x2
B. m3-mn2=m(m+n)(m-n)
C. (y+1)(y-3)=-(3-y)(y+1)
D. 4yz-2y2z+z=2y(2z-yz)+z
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简再求值 ;求代数式2(x2y+xy)-(2xy-x2y)的值,其中x=1,y=-1 ;
相关试题

