Question

【题目】如图，已知直线l1∥l2，直线l3和直线l1，l2分别交于点C和D，点P在直线l3上．

(1)若点P在C，D两点之间运动，∠PAC，∠APB，∠PBD之间的关系是否发生变化？若变化，请说明理由；若不变，请求出它们之间的关系式．

(2)若点P在C，D两点的外侧运动(点P与点C，D不重合)，则∠PAC，∠APB，∠PBD之间的关系又如何？

Answer 1

【答案】（1）∠APB＝∠PAC＋∠PBD；（2）∠PBD＝∠PAC＋∠APB.

【解析】

（1）当P点在C、D之间运动时，首先过点P作PE∥l1，由l1∥l2，可得PE∥l2∥l1，根据两直线平行，内错角相等，即可求得：∠APB=∠PAC+∠PBD；

（2）当点P在C、D两点的外侧运动时，由直线l1∥l2，根据两直线平行，同位角相等与三角形外角的性质，即可求得：∠PBD=∠PAC+∠APB．

（1）不变.当点P在C，D之间运动时，∠APB＝∠PAC＋∠PBD.

理由如下：

如图①，

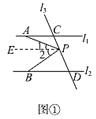
过点P作PE∥l1，

∵l1∥l2，∴PE∥l2∥l1，

∴∠PAC＝∠1，∠PBD＝∠2，

∴∠APB＝∠1＋∠2＝∠PAC＋∠PBD.

（2）如图②，

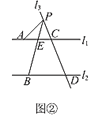
当点P在C，D两点的外侧运动，且在l1上方时，∠PBD＝∠PAC＋∠APB.

理由如下：

∵l1∥l2，

∴∠PEC＝∠PBD.

∵∠PEC＝∠PAC＋∠APB，

∴∠PBD＝∠PAC＋∠APB；

如图③，

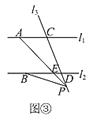
当点P在C，D两点的外侧运动，且在l2下方时，∠PAC＝∠PBD＋∠APB.

理由如下：

∵l1∥l2，

∴∠PED＝∠PAC.

∵∠PED＝∠PBD＋∠APB，

∴∠PAC＝∠PBD＋∠APB.