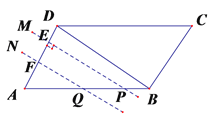
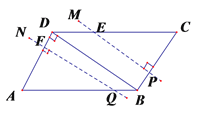
【题目】如图,在□ABCD中,AD=4cm,∠A=60°,BD⊥AD.一动点P从A出发,以每秒1cm的速度沿A→B→C的路线匀速运动,过点P作直线PM,使PM⊥AD.
(1)当点P运动2秒时,设直线PM与AD相交于点E,求△APE的面积;
(2)当点P运动2秒时,另一动点Q也从A出发沿A→B的路线运动,且在AB上以每秒1cm的速度匀速运动,(当P、Q中的某一点到达终点,则两点都停止运动.)过Q作直线QN,使QN∥PM,设点Q运动的时间为t秒(0≤t≤8),直线PM与QN截□ABCD所得图形的面积为S(cm2).求S关于t的函数关系式.

参考答案:
【答案】(1)![]() ;(2)
;(2)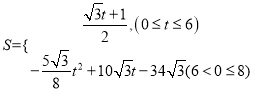 .
.
【解析】试题分析:(1)、根据题意得出AP=2AE,求出当t=2时AP、AE和PE的长度,从而求出△APE的面积;(2)、当点P在AB上时可以得出AQ=t,AP=t+2, ![]() ,
, ![]() ,
, ![]() 从而求出四边形PQFE的面积;当点P在BC上时,根据
从而求出四边形PQFE的面积;当点P在BC上时,根据![]() 得出函数解析式.
得出函数解析式.
试题解析:(1)、∠A=60°,PE⊥AD ∴AP=2AE,
t=2时,AP=2,AE=1,PE=![]() , ∴
, ∴![]() ;
;
(2)、若![]() 时,P在AB上
时,P在AB上
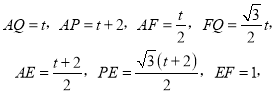
![]()
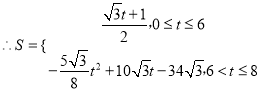 .
.
试题分析:本题主要考查的是动点问题与函数图像结合题,难度中上.在解决有关动点问题的时候,我们一定要注意进行分类讨论,在每一个取值范围之内,我们要将所有的线段用含未知数的代数式来进行表示,然后根据面积的计算法则来求出函数解析式.我们在分类讨论的时候可以多画出几个图形,然后分别进行计算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形ABO中,A(﹣2,﹣3)、B(2,﹣1),三角形A′B′O′是三角形ABO平移之后得到的图形,并且O的对应点O′的坐标为(4,3).
(1)求三角形ABO的面积;
(2)作出三角形ABO平移之后的图形三角形A′B′O′,并写出A′、B′两点的坐标分别为A′ 、B′ ;
(3)P(x,y)为三角形ABO中任意一点,则平移后对应点P′的坐标为__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=3m+2,y=27m﹣8,则用x的代数式表示y为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲口袋中装有3个相同的小球,它们分别写有数值﹣1,1,5;乙口袋中装有3个相同的小球,它们分别写有数值﹣4,2,3.现从甲口袋中随机取一球,记它上面的数值为x,再从乙口袋中随机取一球,记它上面的数值为y.设点A的坐标为(x,y),请用树形图或列表法,求点A落在第一象限的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系xoy中,已知A(6,0),B(8,6),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
(1)写出点C的坐标;
(2)当△ODC的面积是△ABD的面积的3倍时,求点D的坐标;
(3)设∠OCD=α,∠DBA=β,∠BDC=θ,判断α、β、θ之间的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各数中,比﹣1小的数是( )
A.﹣2B.﹣0.5C.0D.1
-
科目: 来源: 题型:
查看答案和解析>>【题目】为支援某灾区,某市民政局组织募捐了240吨救灾物资,现租用甲、乙两种货车,将这批救灾物资一次性全部运往灾区,它们的载货量和租金如下表:
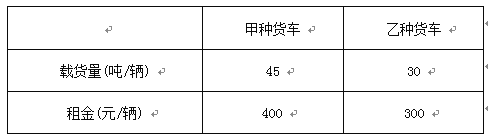
如果计划租用6辆货车,且租车的总费用不超过2 300元,求最省钱的租车方案.
相关试题

