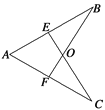
【题目】如图,AE=AF,AB=AC,EC与BF交于点O,∠A=60°,∠B=25°,求∠EOB的度数.
参考答案:
【答案】∠EOB=70°.
【解析】
利用SAS可证明△ABF≌△ACE,根据全等三角形的对应角相等可得∠B=∠C,根据三角形外角的性质得到∠BFC=∠A+∠B,求出∠BFC的度数,在△FOC中,根据三角形的内角和定理求出∠COF的度数,最后根据对顶角相等可得∠EOB的度数.
在△ABF和△ACE中,
∵AF=AE,∠A=∠A,AB=AC,
∴△ABF≌△ACE(SAS).
∴∠B=∠C.
∵∠B=25°,∴∠C=25°.
又∵∠CFB是△AFB的外角,∠A=60°,
∴∠CFB=60°+25°=85°,
∴∠COF=180°-∠CFB-∠C=180°-85°-25°=70°.
又∵∠EOB=∠COF,∴∠EOB=70°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣
 )﹣2+
)﹣2+  ﹣|﹣
﹣|﹣  |+(﹣π)0﹣(﹣1)2015 .
|+(﹣π)0﹣(﹣1)2015 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线顶点坐标为(1,3),且过点A(2,1).

(1)求抛物线解析式;
(2)若抛物线与x轴两交点分别为点B、C,求线段BC的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知AC∥BD,EA,EB分别平分∠CAB和∠DBA,CD过E点.求证:AB=AC+BD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在出行中,主动采用能降低二氧化碳排放量的交通方式,谓之“低碳出行”.明明一家积极响应政府“绿色山城,低碳出行”的号召,今年2月﹣5月明明一家减少了驾车出行,他们将2月﹣5月驾车行驶的里程统计后绘制成以下两幅不完整的统计图:
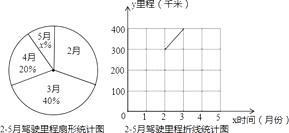
(1)扇形统计图中x= , 并补全折线统计图;
(2)某中学也积极参与“绿色山城,低碳出行”活动中,决定从4名广播社骨干成员中(其中两名男生,两名女生)选拔两名同学去演讲宣传,请用画树形图或列表的方法求所选出的两名同学恰好是一名男生一名女生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠CAB交CD于F,CH⊥EF于H,连接DH,求证:

(1)EH=FH;
(2)∠CAB=2∠CDH. -
科目: 来源: 题型:
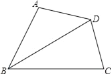
查看答案和解析>>【题目】如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,
求证:∠A+∠C=180°.
相关试题

