搜索
【题目】数学小组的同学为了解“阅读经典”活动的开展情况，随机调查了50名同学，对他们一周的阅读时间进行了统计，并绘制成如图所示的条形统计图，这组数据的中位数和众数分别是（ ）
A.中位数和众数都是8小时
B.中位数是25人，众数是20人
C.中位数是13人，众数是20人
D.中位数是6小时，众数是8小时
参考答案：
【答案】A
【解析】因数据总数为50，故中位数为第25和26个数据的平均数，而条形统计图是按从小到大的顺序排列的，前3组的和为24，前4组的和为44，
故第25和26个数据落在第4组，故中位数是8（小时）；
条形统计图中出现频数最大的条形对应第四组，故众数是8（小时）；
所以答案是：A．
【考点精析】认真审题，首先需要了解中位数、众数(中位数是唯一的，仅与数据的排列位置有关，它不能充分利用所有数据；众数可能一个，也可能多个，它一定是这组数据中的数)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列运算正确的是（ ）
A.（a2）3＝a6B.（ab）2＝ab2C.a2+a2＝a4D.aa2＝a2
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数
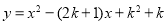（k＞0）．（1）当k=
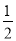时，求这个二次函数的顶点坐标；（2）求证：关于x的一元次方程
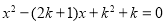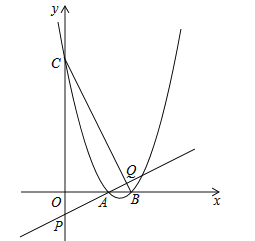
有两个不相等的实数根；（3）如图，该二次函数与x轴交于A、B两点（A点在B点的左侧），与y轴交于C点，P是y轴负半轴上一点，且OP=1，直线AP交BC于点Q，求证：
．
-
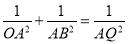科目： 来源： 题型：
查看答案和解析>>【题目】某网店打出促销广告：最潮新款服装30件，每件售价300元．若一次性购买不超过10件时，售价不变；若一次性购买超过10件时，每多买1件，所买的每件服装的售价均降低3元．已知该服装成本是每件200元，设顾客一次性购买服装x件时，该网店从中获利y元．
（1）求y与x的函数关系式，并写出自变量x的取值范围；
（2）顾客一次性购买多少件时，该网店从中获利最多？
-
科目： 来源： 题型：
查看答案和解析>>【题目】据电力部门统计，每天8：00至21：00是用电的高峰期，简称“峰时”，21：00至次日8：00是用电的低谷时期，简称“谷时”，为了缓解供电需求紧张矛盾，某市电力部门于本月初统一换装“峰谷分时”电表，对用电实行“峰谷分时电价”新政策，具体见下表：
（1）小张家上月“峰时”用电50度，“谷时”用电20度，若上月初换表，则相对于换表前小张家的电费是增多了还是减少了？增多或减少了多少元？请说明理由．
（2）小张家这个月用电95度，经测算比换表前使用95度电节省了5.9元，问小张家这个月使用“峰时电”和“谷时电”分别是多少度？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，点D，E分别是AB，AC的中点，∠A=50°，∠ADE=60°，则∠C的度数为（ ）
A.50°
B.60°
C.70°
D.80° -
科目： 来源： 题型：
查看答案和解析>>【题目】为支持国家南水北调工程建设，小王家由原来养殖户变为种植户，经市场调查得知，种植草莓不超过20亩时，所得利润y（元）与种植面积m（亩）满足关系式y=1500m；超过20亩时，y=1380m+2400．而当种植樱桃的面积不超过15亩时，每亩可获得利润1800元；超过15亩时，每亩获得利润z（元）与种植面积x（亩）之间的函数关系如下表（为所学过的一次函数、反比例函数或二次函数中的一种）．
（1）设小王家种植x亩樱桃所获得的利润为P元，直接写出P关于x的函数关系式，并写出自变量的取值范围；
（2）如果小王家计划承包40亩荒山种植草莓和樱桃，当种植樱桃面积x（亩）满足0＜x＜20时，求小王家总共获得的利润w（元）的最大值．
相关试题
