【题目】用适当的方法解下列方程:
(1) ![]() (2)2x2+3x—1=0(用配方法解)
(2)2x2+3x—1=0(用配方法解)
(3) ![]() (4)(x+1)(x+8)=-2
(4)(x+1)(x+8)=-2
(5) ![]() (6)
(6) ![]()
参考答案:
【答案】(1)x1=0,x2=4;(2)x1=![]() ,x2=
,x2=![]() ;(3)x1=2,x2=3;(4)x1=
;(3)x1=2,x2=3;(4)x1=![]() ,x2=
,x2=![]() ;(5)x1=1,x2=—2;(6)
;(5)x1=1,x2=—2;(6)![]() ,
,![]() .
.
【解析】(1)方程变形后,开方即可求出解;(2)利用配方法解方程,先将系数化为1,再将方程两边同时加一次项系数一半的平方,即可求解;(3)先移项,再提公因式化为两个因式相乘的形式,进而求解;(4)首先整理,然后找出a、b、c的值,利用求根公式得出答案;(5)设y=x+x,则原方程可化为2y-3=![]() ,解方程求得y的值,再代入x+x=y,求出x的值即可;(6)利用代入法求解即可.
,解方程求得y的值,再代入x+x=y,求出x的值即可;(6)利用代入法求解即可.
(1) ![]() ,
,
变形得:![]() ,
,
开方得:x-2=2或x-2=-2,
解得: x1=0,x2=4;
(2)解:![]() ,
,
![]() ,
,![]() ,(x+
,(x+![]() )=
)=![]() ,x+
,x+![]() =±
=±![]() ,
,
![]() ,
,![]() .
.
(3)![]() ,(x-2)(3x-6-x)=0,即x-2=0或3x-6-x=0,解得:x1=2,x2=3.
,(x-2)(3x-6-x)=0,即x-2=0或3x-6-x=0,解得:x1=2,x2=3.
(4) (x+1)(x+8)=-2,x+9x+10=0, 由a=1,b=9,c=10, ∵b-4ac=81-40=41,
∴x=![]() ∴x1=
∴x1=![]() ,x2=
,x2=![]() .
.
(5) ![]() ,设x+x=y, 则2y-3=
,设x+x=y, 则2y-3=![]() , 2y-3y=2,(y-2)(2y+1)=0,
, 2y-3y=2,(y-2)(2y+1)=0,![]() ,
,
当x+x=2,解得:x1=1,x2=—2 ;当x+x=![]() ,2x+2x+1=0,b-4ac<0, ∴此方程无解;
,2x+2x+1=0,b-4ac<0, ∴此方程无解;
经检验原方程的解为:x1=1,x2=—2;
(6)![]() ,由①得y=x-3③,把③代入②得:x+x-2=0,解得
,由①得y=x-3③,把③代入②得:x+x-2=0,解得![]() .分别代入③得
.分别代入③得![]() ,∴原方程的解为:
,∴原方程的解为:![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4). (Ⅰ)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(Ⅱ)以点O为位似中心,将△ABC缩小为原来的 ,得到△A2B2C2 , 请在图中y轴右侧,画出△A2B2C2 , 并求出∠A2C2B2的正弦值.
,得到△A2B2C2 , 请在图中y轴右侧,画出△A2B2C2 , 并求出∠A2C2B2的正弦值.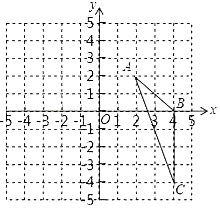
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
(1)某文艺团体组织了一场义演为“希望工程”募捐,共售出1000张门票,已知成人票每张8元,学生票每张5元,共得票款6950元,成人票和学生票各几张
(2)某地生产一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元;经粗加工后销售,每吨利润可达4500元;经精加工后销售,每吨利润涨至7500元.当地一家农工商公司收获这种蔬菜140吨,该公司加工的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行.受季节等条件限制,公司必须在15天内将这批蔬菜全部销售或加工完毕,为此公司研制了三种可行方案.
方案一:将蔬菜全部进行精加工.没来得及进行精加工的直接出售
方案二:尽可能多地对蔬菜进行粗加工,没有来得及进行加工的蔬菜,在市场上直接销售.
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好15天完成.
你认为选择哪种方案获利最多?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F. (Ⅰ)试判断直线BC与⊙O的位置关系,并说明理由;
(Ⅱ)若BD=2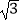 ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).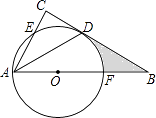
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆客车、一辆货车和一辆小轿车在一条笔直的公路上朝同一方向匀速行驶,在某一时刻,客车在前,小轿车在后,货车在客车与小轿车的正中间,过了12分钟,小轿车追上了货车,又过了8分钟,小轿车追上了客车,再过t分钟,货车追上了客车,则t=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD,M、N两动点分别从A.C两点同时出发沿正方形的边开始移动,点M按逆时针方向移动,点N按顺时针方向移动,若点M的速度是点N的4倍,则它们第2018次相遇在边_____上.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)2x+5=3
(2)6x﹣7=4x﹣5;
(3)4x+3(12﹣x)=6
(4)
 .
.
相关试题

