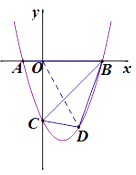
【题目】如图(1),抛物线y=ax2+bx+c与x轴交于A(x1,0)、B(x2,0)两点(x1<0<x2),与y轴交于点C(0,-3),若抛物线的对称轴为直线x=1,且tan∠OAC=3.
(1)求抛物线的函数解析式;
(2)若点D是抛物线BC段上的动点,且点D到直线BC距离为 ![]() ,求点D的坐标
,求点D的坐标
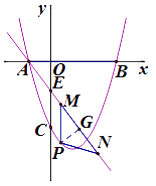
(3)如图(2),若直线y=mx+n经过点A,交y轴于点E(0, - ![]() ),点P是直线AE下方抛物线上一点,过点P作x轴的垂线交直线AE于点M,点N在线段AM延长线上,且PM=PN,是否存在点P,使△PMN的周长有最大值?若存在,求出点P的坐标及△PMN的周长的最大值;若不存在,请说明理由.
),点P是直线AE下方抛物线上一点,过点P作x轴的垂线交直线AE于点M,点N在线段AM延长线上,且PM=PN,是否存在点P,使△PMN的周长有最大值?若存在,求出点P的坐标及△PMN的周长的最大值;若不存在,请说明理由.
参考答案:
【答案】
(1)
在Rt△AOC中,tan ![]() OAC=
OAC= ![]() =3,且OC=3,
=3,且OC=3,
∴OA=1,A(-1,0)
∵抛物线的对称轴为直线x=1
∴由中点坐标公式可求: ![]() ,解得x=3
,解得x=3
∴B(3,0)
∴可设抛物线的表达式为:y=a(x-3)(x+1)
将C(0,-3)代入上式中,a×(-3)=-3,
解得:a=1
∴抛物线的表达式为:y=(x-3)(x+1)=x2-2x-3
(2)
∵B(3,0)、C(0,-3)
∴ ![]()
∴ ![]()
设D(x,x2-2x-3).连接OD.
∴ ![]()
= ![]()
= ![]()
= ![]()
=3
解得:x1=1,x2=2
∴D(1,-4)(2,-3)
(3)
由A(-1,0)、E(0,- ![]() )可求:
)可求:
直线AE的表达式为:y= ![]() ,AE=
,AE= ![]()
设p(t,t2-2t-3),则M(t, ![]() t
t ![]() )
)
∴PM= ![]() t
t ![]() -(t2-2t-3)=- t2+
-(t2-2t-3)=- t2+ ![]()
作PG⊥MN于G,
由PM=PN得:MG=NG= ![]() MN
MN
由△PMG∽△AEO有: ![]() ,即
,即 ![]()
∴MG= ![]() PM=NG
PM=NG
∴C△PMN=PM+PN+MN= ![]() PM=
PM= ![]() (- t2+
(- t2+ ![]() )=-
)=- ![]() t2+
t2+ ![]() t+6
t+6
∴当t= ![]() 时,C△PMN有最大值为
时,C△PMN有最大值为 ![]() ,此时P
,此时P ![]()
【解析】(1)C点的坐标已知,tan∠OAC,据此求出A点坐标;对称轴是x=1,据此求出B点坐标。(2)B、C两点的坐标是已知,根据两点之间的距离公式求出BC的长度,点D到直线BC的距离为 ![]() ,根据
,根据 ![]() BCD的面积求出D点的坐标。(3)已知A、E两点的坐标,可以先求出直线AE的表达式。易知P、M的横坐标相同,分别设出P、M两点。用PM分别表示出PN,MN,根据二次函数的性质,求出
BCD的面积求出D点的坐标。(3)已知A、E两点的坐标,可以先求出直线AE的表达式。易知P、M的横坐标相同,分别设出P、M两点。用PM分别表示出PN,MN,根据二次函数的性质,求出 ![]() PMN周长的最大值及此时P点的坐标。
PMN周长的最大值及此时P点的坐标。
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△AOB中,A(-8,0),B(0,
 ),AC平分∠OAB,交y轴于点C,点P是x轴上一点,⊙P经过点A、C,与x轴于点D,过点C作CE⊥AB,垂足为E,EC的延长线交x轴于点F,
),AC平分∠OAB,交y轴于点C,点P是x轴上一点,⊙P经过点A、C,与x轴于点D,过点C作CE⊥AB,垂足为E,EC的延长线交x轴于点F,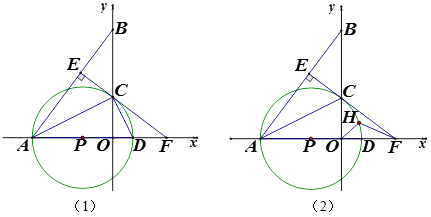
(1)求⊙P的半径;
(2)求证:EF为⊙P的切线;
(3)若点H是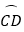 上一动点,连接OH、FH,当点P在
上一动点,连接OH、FH,当点P在 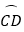 上运动时,试探究
上运动时,试探究 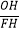 是否为定值?若为定值,求其值;若不是定值,请说明理由.
是否为定值?若为定值,求其值;若不是定值,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某运动品牌对第一季度A、B两款运动鞋的销售情况进行统计,两款运动鞋的销售量及总销售额如图10所示:
(1)一月份B款运动鞋的销售量是A款的
 ,则一月份B款运动鞋销售了多少双?
,则一月份B款运动鞋销售了多少双?(2)第一季度这两款运动鞋的销售单价保持不变,求三月份的总销售额(销售额=销售单价×销售量);
(3)结合第一季度的销售情况,请你对这两款运动鞋的进货、销售等方面提出一条建议。

-
科目: 来源: 题型:
查看答案和解析>>【题目】学期结束前,学校想调查学生对七年级数学实验教材的意见,特向七年级400名学生作问卷调查,其结果如下:
(1)计算出每一种意见的人数占调查人数的百分比;
(2)从统计图中你能得出什么结论?
意见
非常喜欢
喜欢
有一点喜欢
不喜欢
人数
200
160
32
8
-
科目: 来源: 题型:
查看答案和解析>>【题目】若顺次连接四边形ABCD各边中点所得四边形是矩形,则四边形ABCD必然是( )
A.菱形
B.对角线相互垂直的四边形
C.正方形
D.对角线相等的四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD边上以每秒1cm 的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有__次.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点,则函数y=ax2+(b﹣1)x+c的图象可能是( )

A.
B.
C.
D.
相关试题

