搜索
【题目】如图，在四边形ABCD中，AD∥BC，AD=8，BC=16，点P以每秒1个单位长度的速度从点A出发，沿AD向点D运动；点Q同时以每秒2个单位长度的速度从点C出发，沿CB向点B运动，点P停止运动时，点Q也随之停止运动，设运动时间为t秒．
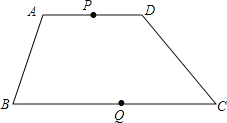
（1）当t为多少时，以点ABQD为顶点的四边形是平行四边形？
（2）当t为多少时，以点ABQP为顶点的四边形是平行四边形？
参考答案：
【答案】（1）t为4秒时（2）t为
秒时
【解析】
试题分析：（1）当四边形ABQD为平行四边形时，AD=BQ=8，由题意得出方程，解方程即可；
（2）当四边形ABQP为平行四边形时，AP=BQ； 由题意得出方程，解方程即可．
解：（1）∵当四边形ABQD为平行四边形时，AD=BQ=8，
又∵Q点速度为2个单位/秒，
∴16﹣2t=8，
解得：t=4，
即当t为4秒时，以点ABQD为顶点的四边形是平行四边形；
（2）∵当四边形ABQP为平行四边形时，AP=BQ；
又∵点P、Q速度分别为1个单位/秒、2个单位/秒，AD=8，BC=16，
∴t=16﹣2t，
解得：t=，
即当t为秒时，以点ABQP为顶点的四边形是平行四边形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】 如图，在平面直角坐标系中直线y=x﹣2与y轴相交于点A，与反比例函数在第一象限内的图象相交于点B（m，2）．
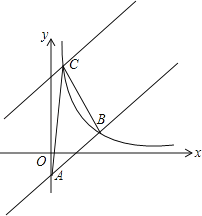
（1）求反比例函数的关系式；
（2）将直线y=x﹣2向上平移后与反比例函数图象在第一象限内交于点C，且△ABC的面积为18，求平移后的直线的函数关系式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线y=﹣x2+bx+c经过A（0，1）、B（4，3）两点．
（1）求抛物线的解析式；
（2）求tan∠ABO的值；
（3）过点B作BC⊥x轴，垂足为C，点M是抛物线上的一个动点，直线MN平行于y轴交直线AB于N，如果M、N、B、C为顶点的四边形是平行四边形，请直接写出M点的横坐标；
（4）已知点E为抛物线上位于第二象限内任一点，且E点横坐标为m，作边长为10的正方形EFGH，使EF∥x轴，点G在点E的右上方，那么，对于大于或等于﹣1的任意实数m，FG边与过A、B两点的直线都有交点，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】把几个图形拼成一个新的图形，再通过两种不同的方法计算同一个图形的面积，可以得到一个等式，也可以求出一些不规则图形的面积．
例如，由图1，可得等式：（a+2b）（a+b）=a2+3ab+2b2
（1）如图2，将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形，试用不同的形式表示这个大正方形的面积，你能发现什么结论？请用等式表示出来．
（2）利用（1）中所得到的结论，解决下面的问题： 已知a+b+c=11，ab+bc+ac=38，求a2+b2+c2的值．
（3）如图3，将两个边长分别为a和b的正方形拼在一起，B，C，G三点在同一直线上，连接BD和BF．若这两个正方形的边长满足a+b=10，ab=20，请求出阴影部分的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，点E在AD上，且EC平分∠BED。
（1）△BEC是否是等腰三角形？证明你的结论。
（2）若AB=1，∠ABE=450，求矩形ABCD的面积。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将周长为8的△ABC沿BC方向平移1个单位长度得到
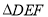，则四边形
的周长为（ ）
A. 8 B. 10 C. 12 D. 16
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，AB是⊙O的直径，AE是弦，C是劣弧AE的中点，过C作CD⊥AB于点D，CD交AE于点F，过C作CG∥AE交BA的延长线于点G．
（1）求证：CG是⊙O的切线．
（2）求证：AF=CF．
（3）若∠EAB=30°，CF=2，求GA的长．
相关试题
