【题目】某校数学综合实践小组的同学以“绿色出行”为主题,把某小区的居民对共享单车的了解和使用情况进行了问卷调查,在这次调查中,发现有20人对于共享单车不了解,使用共享单车的居民每天骑行路程不超过8千米,并将调查结果制作成统计图,如图所示. 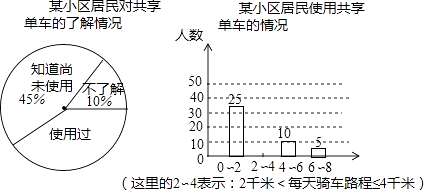
(1)本次调查人数共人 , 使用过共享单车的有人;
(2)请将条形统计图补充完整;
(3)如果这个小区大约有3000名居民,请估算出每天的骑行路程在2~4千米的有多少人?
参考答案:
【答案】
(1)200;90
(2)骑行距离在第二组的人数是90﹣25﹣10﹣5=50.

(3)每天的骑行路程在2~4千米的有3000× ![]() =750(人).
=750(人).
答:每天的骑行路程在2~4千米的有750人
【解析】解:(1)调查的人数是20÷10%=200; 使用过共享单车的人数少是:200×(1﹣45%﹣10%)=90.
故答案是:200,90;
(1)根据有20人对于共享单车不了解,所占的百分比是10%,据此即可求得调查的总人数,利用总人数乘以对应的百分比求得使用过单车的人数;(2)利用使用过单车的人数减去其它组的人数即可求得第二组的人数,从而补全直方图;(3)利用总人数乘以对应的比例即可求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列一元一次方程解应用题:
2018年是我国改革开放40周年,改革开放是当代中国发展进步的必由之路,是实现中国梦的必由之路. 2018年10月20日在国家大剧院举行了《可爱的中国》庆祝改革开放40周年音乐会. 本次演出的票价分为以下几个类别,如下表所示:
演出票类别
A类
B类
C类
D类
E类
演出票单价(元/张)
300
280
240
180
100
小宇购买了A类和C类的演出票共10张,他发现这10张演出票的总价恰好可以购买8张B类票和4张E类票. 问小宇购买A类和C类的演出票各几张?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于数轴上不重合的两点A,B,给出如下定义:若数轴上存在一点M,通过比较线段AM和BM的长度,将较短线段的长度定义为点M到线段AB的“绝对距离”. 若线段AM和BM的长度相等,将线段AM或BM的长度定义为点M到线段AB的“绝对距离”.
(1)当数轴上原点为O,点A表示的数为-1,点B表示的数为5时.
①点O到线段AB的“绝对距离”为____;
②点M表示的数为
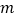 ,若点M到线段AB的“绝对距离”为3,则
,若点M到线段AB的“绝对距离”为3,则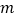 的值为______;
的值为______;(2)在数轴上,点P表示的数为-6,点A表示的数为-3,点B表示的数为2. 点P以每秒2个单位长度的速度向正半轴方向移动时,点B同时以每秒1个单位长度的速度向负半轴方向移动. 设移动的时间为
 秒,当点P到线段AB的“绝对距离”为2时,求
秒,当点P到线段AB的“绝对距离”为2时,求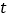 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各式分解因式:
(1)
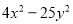 (2)
(2) 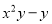
(3)
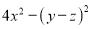 (4)
(4)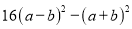
(5)
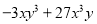 (6)
(6) 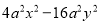
(7)
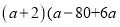 (8)
(8) 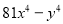
(9)
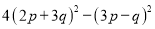 (10)
(10) 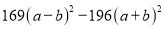
-
科目: 来源: 题型:
查看答案和解析>>【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从①∠1=∠2;②∠C=∠D;③∠A=∠F三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )

A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
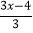 -
-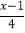 =1-
=1-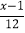
解:去分母,得_________________________________.
去括号,得___________________________.
移项,得___________________________.
合并同类项,得__________.
两边都除以______,得x=_______.
相关试题

