Question

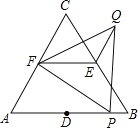
【题目】如图，△ABC和△FPQ均是等边三角形，点D、E、F分别是△ABC三边的中点，点P在AB边上，连接EF、QE．若AB=6，PB=1，则QE= ．

Answer 1

【答案】2.

【解析】

试题分析：连结FD，根据等边三角形的性质，由△ABC为等边三角形得到AC=AB=6，∠A=60°，再根据点D、E、F分别是等边△ABC三边的中点，则AD=BD=AF=3，DP=2，EF为△ABC的中位线，于是可判断△ADF为等边三角形，得到∠FDA=60°，利用三角形中位线的性质得EF∥AB，EF=AB=3，根据平行线性质得∠1+∠3=60°；又由于△PQF为等边三角形，则∠2+∠3=60°，FP=FQ，所以∠1=∠2，然后根据“SAS”判断△FDP≌△FEQ，所以DP=QE=2．

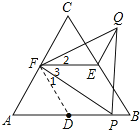
解：连结FD，如，

∵△ABC为等边三角形，

∴AC=AB=6，∠A=60°，

∵点D、E、F分别是等边△ABC三边的中点，AB=6，PB=1，

∴AD=BD=AF=3，DP=DB﹣PB=3﹣1=2，EF为△ABC的中位线，

∴EF∥AB，EF=AB=3，△ADF为等边三角形，

∴∠FDA=60°，

∴∠1+∠3=60°，

∵△PQF为等边三角形，

∴∠2+∠3=60°，FP=FQ，

∴∠1=∠2，

∵在△FDP和△FEQ中

，

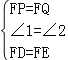∴△FDP≌△FEQ（SAS），

∴DP=QE，

∵DP=2，

∴QE=2．

故答案为：2．