【题目】如图,BD是□ABCD的一条对角线.AE⊥BD于点E,CF⊥BD于点F.求证:∠DAE=∠BCF.

参考答案:
【答案】见解析
【解析】试题分析:由四边形ABCD为平行四边形,根据平行四边形的对边平行且相等得到AD=BC,AD∥BC,由两直线平行,内错角相等可得∠ADB=∠CBD,再由AE⊥BD,CF⊥BD得∠AED=∠CFB=90°,利用AAS证得△ADE≌△CBF,利用全等三角形的对应角相等即可得∠DAE=∠BCF.
试题解析:
证明:∵平行四边形ABCD,
∴AD=BC,AD∥BC,
∴∠ADB=∠CBD,
∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB=90°,
在△ADE和△CBF中, 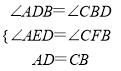 ,
,
∴△ADE≌△CBF(AAS),
∴∠DAE=∠BCF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,按下列条件得到的四边形EFGH不一定是平行四边形的是( )
A.
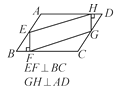
B.

C.

D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场对一种新售的手机进行市场问卷调查,其中一个项目是让每个人按A(不喜欢)、B(一般)、C(不比较喜欢)、D(非常喜欢)四个等级对该手机进行评价,图①和图②是该商场采集数据后,绘制的两幅不完整的统计图,请你根据以上统计图提供的信息,回答下列问题:
(1)本次调查的人数为多少人?A等级的人数是多少?请在图中补全条形统计图.
(2)图①中,a等于多少?D等级所占的圆心角为多少度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以△ABC的两条边为边做平行四边形,所做的平行四边形有____ __个;
平行四边形第四个顶点的坐标是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为( )

A.78°
B.75°
C.60°
D.45° -
科目: 来源: 题型:
查看答案和解析>>【题目】4月的某天小欣在“A超市”买了“雀巢巧克力”和“趣多多小饼干”共10包,已知“雀巢巧克力”每包22元,“趣多多小饼干”每包2元,总共花费了80元.
(1)请求出小欣在这次采购中,“雀巢巧克力”和“趣多多小饼干”各买了多少包?
(2)“五一”期间,小欣发现,A、B两超市以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在A超市累计购物超过50元后,超过50元的部分打九折;在B超市累计购物超过100元后,超过100元的部分打八折.
①请问“五一”期间,若小欣购物金额超过100元,去哪家超市购物更划算?
②“五一”期间,小欣又到“B超市”购买了一些“雀巢巧克力”,请问她至少购买多少包时,平均每包价格不超过20元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果三角形满足一个角是另一个角的3倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能作为一个智慧三角形三边长的一组是( )
A.1,2,3
B.1,1,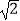
C.1,1,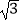
D.1,2,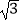
相关试题

