【题目】如图,⊙![]() 是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙
是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙![]() 于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF。
于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF。
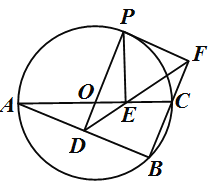
(1)、若∠POC=60°,AC=12,求劣弧PC的长;(结果保留π)
(2)、求证:OD=OE;
(3)、求证:PF是⊙![]() 的切线。
的切线。
参考答案:
【答案】(1)、2π;(2)、证明过程见解析;(3)、证明过程见解析.
【解析】试题分析:(1)、根据直径得出半径的长度,然后根据弧长的计算公式进行求解;(2)、根据垂直得出∠ADO=∠PEO,对顶角相等,半径相等得出△ADO和△PEO全等,从而得出OD=OE;(3)、连接PC,根据直径得出∠ABC=90°,从而说明PD∥BC,根据已知条件结合(2)得出△PCE和△PFC全等,从而说明∠OPF=90°,得出切线.
试题解析:(1)、由直径AC=12得半径OC=6 劣弧PC的长为![]()
(2)、∵ OD⊥AB,PE⊥AC ∴ ∠ADO=∠PEO=90°
在△ADO和△PEO中,∠ADO=∠PEO,∠AOD=∠POE,OA=OP ∴ △ADO≌△PEO ∴ OD=OE
(3)、连接PC,由AC是直径知BC⊥AB,又OD⊥AB, ∴ PD∥BF
∴ ∠OPC=∠PCF,∠ODE=∠CFE 由(2)知OD=OE,则∠ODE=∠OED,又∠OED=∠FEC
∴ ∠FEC=∠CFE ∴ EC=FC 由OP=OC知∠OPC=∠OCE
∴ ∠PCE =∠PCF 在△PCE和△PFC中, EC=FC ∠PCE=∠PCF PC=PC
∴ △PCE≌△PFC ∴ ∠PFC =∠PEC=90° 由∠PDB=∠B=90°可知∠OPF=90°即OP⊥PF
∴ PF是⊙![]() 的切线
的切线
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解方程x2+8x+7=0,则配方正确的是( )
A.(x+4)2=9
B.(x﹣4)2=9
C.(x﹣8)2=16
D.(x+8)2=57 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)。请你根据他们测量数据计算这棵树CD的高度(结果精确到0.1m)。(参考数据:
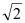 ≈1.414,
≈1.414,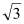 ≈1.732)
≈1.732)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图1和图2所示的不完整的统计图。

(1)这次被调查的同学共有 名;
(2)把条形统计图(题22-1图)补充完整;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐。据此估算,该校18 000名学生一餐浪费的食物可供多少人食用一餐?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a<b,则下列不等式中不正确的是( )
A. 4a<4b B. a+4<b+4 C. ﹣4a<﹣4b D. a﹣4<b﹣4
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个数是10,另一个数比10的相反数小2,则这两个数的和为( )
A. 18 B. 2 C. -18 D. -2
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:2x2-2=___________________。
相关试题

