【题目】如图,AD是△ABC的高线,在BC边上截取点E,使得CE=BD,过E作EF∥AB,过C作CP⊥BC交EF于点P。过B作BM⊥AC于M,连接EM、PM。
(1)依题意补全图形;
(2)若AD=DC,探究EM与PM的数量关系与位置关系,并加以证明。

参考答案:
【答案】(1)见解析;(2)EM⊥PM,EM=PM,证明见解析.
【解析】
(1)根据要求画出图形即可;
(2)连接MD,证明△ABD≌△PEC,则AD=PC,可得出PC=DC,再证△DCM≌△PCM,则MD=MP,∠PMC=∠DMC,再证△MDB≌△MEC,则MD=ME,∠BMD=∠CME,即可得出EM与PM的数量关系与位置关系.
解:(1)补全的图形如图所示;
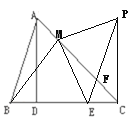
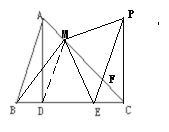
(2)EM⊥PM,EM=PM.
证明:连接DM,∵EF∥AB,∴∠ABD=∠PEC,
∵AD是△ABC的高线,CP⊥BC,
∴∠ADB=∠PCE=90°,
∵BD=EC,
∴△ABD≌△PEC,
∴AD=PC,
∵AD=DC,
∴PC=DC,
∵AD是△ABC的高线,CP⊥BC,AD=DC,
∴∠ACD=∠ACP=45°,
又∵CM=CM,
∴△DCM≌△PCM,
∴MD=MP,∠PMC=∠DMC;
∵BM⊥AC,∠ACD=45°,
∴MB=MC,∠ACD=∠MBC=45°,
又∵BD=CE,
∴△MDB≌△MEC,
∴MD=ME,∠BMD=∠CME,
∴MP=ME;
∵BM⊥AC,
∴∠BMD +∠DMC=90°,
∵∠BMD=∠CME,∠PMC=∠DMC,
∴∠CME +∠PMC =90°,即MP⊥ME,
∴EM与PM的数量关系与位置关系是:EM⊥PM,EM=PM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形
 中,对角线
中,对角线 与
与 相交于点
相交于点 .要使四边形
.要使四边形 是正方形,还需添加一组条件.下面给出了五组条件:①
是正方形,还需添加一组条件.下面给出了五组条件:① ,且
,且 ;②
;② , 且
, 且 ;③
;③ ,且
,且 ;④
;④ ,且
,且 ;⑤
;⑤ ,且
,且 .其中正确的是________(填写序号).
.其中正确的是________(填写序号). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, 为
为 边上的中线,
边上的中线,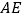 ∥
∥ ,且
,且 ,连接
,连接 .
.(1)求证:四边形
 为菱形;
为菱形;(2)连接
 ,若
,若 平分
平分 ,
, ,求
,求 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在等边△ABC中, AB=
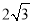 , D,E分别是AB,BC的中点(如图).若将△BDE绕点B逆时针旋转,得到△BD1E1,设旋转角为α(0°<α<180°),记射线CE1与AD1的交点为P.点P到BC所在直线的距离的最大值为_____________.
, D,E分别是AB,BC的中点(如图).若将△BDE绕点B逆时针旋转,得到△BD1E1,设旋转角为α(0°<α<180°),记射线CE1与AD1的交点为P.点P到BC所在直线的距离的最大值为_____________.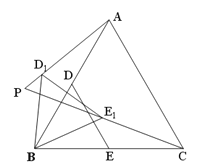
-
科目: 来源: 题型:
查看答案和解析>>【题目】某教研机构为了了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成不完整的统计表,请根据图表中的信息解答下列问题.
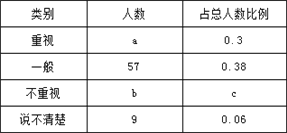
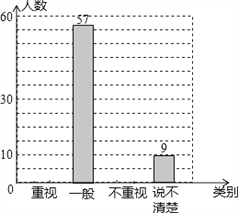
(1)样本容量为 ,表格中c的值为 ,并补全统计图;
(2)若该校共有初中生2300名,请估计该校“不重视阅读数学教科书”的初中人数为 ;
(3)根据上面的数据统计结果,谈谈你对该校初中生阅读数学教科书的现状的看法及建议;如果要了解全省初中生阅读数学教科书的情况,你认为应该如何进行抽样?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数
 的图像与反比例函数
的图像与反比例函数 的图像交于第一、三象限内的
的图像交于第一、三象限内的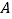 、
、 两点,与
两点,与 轴交于点
轴交于点 ,点
,点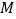 在
在 轴负半轴上,
轴负半轴上, ,且四边形
,且四边形 是平行四边形,点
是平行四边形,点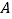 的纵坐标为
的纵坐标为 .
.(1)求该反比例函数和一次函数的表达式;
(2)连接
 ,求
,求 的面积;
的面积;(3)直接写出关于
 的不等式
的不等式 的解集.
的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种情况是等可能的,当三辆汽车经过这个十字路口时:
(1)请你用列表或画树状图的方法,表示出所有可能的结果;
(2)三辆车全部同向而行的概率是 ,至少有两辆车向左转的概率是 ;
(3)由于十字路口右拐弯处是通往新建经济开发区的,因此交管部门在汽车行驶高峰时段对车流量作了统计,发现汽车在此十字路口向右转的频率为
 ,向左转和直行的频率均为
,向左转和直行的频率均为 .目前在此路口,汽车左转、右转、直行的绿灯亮的时间分别为30秒,在绿灯亮总时间不变的条件下,为了缓解交通拥挤,请你用统计的知识对此路口三个方向的绿灯亮的时间做出合理的调整.
.目前在此路口,汽车左转、右转、直行的绿灯亮的时间分别为30秒,在绿灯亮总时间不变的条件下,为了缓解交通拥挤,请你用统计的知识对此路口三个方向的绿灯亮的时间做出合理的调整.
相关试题

