【题目】如图 1,直线![]() 分别交
分别交![]() 于点
于点![]() (点
(点![]() 在点
在点![]() 的右侧),若
的右侧),若![]()
(1)求证:![]() ;
;

(2)如图2所示,点![]() 在
在![]() 之间,且位于
之间,且位于![]() 的异侧,连
的异侧,连![]() , 若
, 若![]() ,则
,则![]() 三个角之间存在何种数量关系,并说明理由.
三个角之间存在何种数量关系,并说明理由.

(3)如图 3 所示,点![]() 在线段
在线段![]() 上,点
上,点![]() 在直线
在直线![]() 的下方,点
的下方,点![]() 是直线
是直线![]() 上一点(在
上一点(在![]() 的左侧),连接
的左侧),连接![]() ,若
,若![]() ,则请直接写出
,则请直接写出![]() 与
与![]() 之间的数量
之间的数量

参考答案:
【答案】(1)证明过程见解析;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]() ∠N+∠PMH=180°.
∠N+∠PMH=180°.
【解析】
(1)根据同旁内角互补,两直线平行即可判定AB∥CD;
(2)设∠N=![]() ,∠M=
,∠M=![]() ,∠AEM=
,∠AEM=![]() ,∠NFD=
,∠NFD=![]() ,过M作MP∥AB,过N作NQ∥AB可得∠PMN=
,过M作MP∥AB,过N作NQ∥AB可得∠PMN=![]() -
-![]() ,∠QNM=
,∠QNM=![]() -
-![]() ,根据平行线性质得到
,根据平行线性质得到![]() -
-![]() =
=![]() -
-![]() ,化简即可得到
,化简即可得到![]() ;
;
(3)过点M作MI∥AB交PN于O,过点N作NQ∥CD交PN于R,根据平行线的性质可得∠BPM=∠PMI,由已知得到∠MON=∠MPN+∠PMI=3∠PMI及∠RFN=180°-∠NFH-∠HFD=180°-3∠HFD,根据对顶角相等得到∠PRF=∠FNP+∠RFN=∠FNP+180°-3∠RFM,化简得到∠FNP+2∠PMI-2∠RFM=180°-∠PMH,根据平行线的性质得到3∠PMI+∠FNP+∠FNH=180°及3∠RFM+∠FNH=180°,两个等式相减即可得到∠RFM-∠PMI=![]() ∠FNP,将该等式代入∠FNP+2∠PMI-2∠RFM=180°-∠PMH,即得到
∠FNP,将该等式代入∠FNP+2∠PMI-2∠RFM=180°-∠PMH,即得到![]() ∠FNP=180°-∠PMH,即
∠FNP=180°-∠PMH,即![]() ∠N+∠PMH=180°.
∠N+∠PMH=180°.
(1)证明:∵∠1=∠BEF,![]()
∴∠BEF+∠2=180°
∴AB∥CD.
(2)解:![]()
设∠N=![]() ,∠M=
,∠M=![]() ,∠AEM=
,∠AEM=![]() ,∠NFD=
,∠NFD=![]()
过M作MP∥AB,过N作NQ∥AB
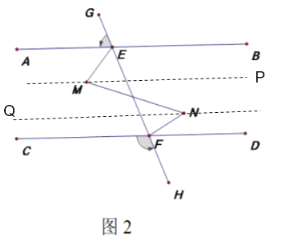
∵![]() ,MP∥AB,NQ∥AB
,MP∥AB,NQ∥AB
∴MP∥NQ∥AB∥CD
∴∠EMP=![]() ,∠FNQ=
,∠FNQ=![]()
∴∠PMN=![]() -
-![]() ,∠QNM=
,∠QNM=![]() -
-![]()
∴![]() -
-![]() =
=![]() -
-![]()
即![]() =
=![]() -
-![]()
∴![]()
故答案为![]()
(3)解:![]() ∠N+∠PMH=180°
∠N+∠PMH=180°
过点M作MI∥AB交PN于O,过点N作NQ∥CD交PN于R.
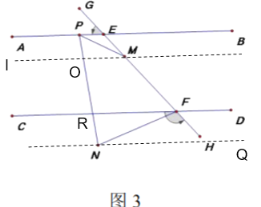
∵![]() ,MI∥AB,NQ∥CD
,MI∥AB,NQ∥CD
∴AB∥MI∥NQ∥CD
∴∠BPM=∠PMI
∵∠MPN=2∠MPB
∴∠MPN=2∠PMI
∴∠MON=∠MPN+∠PMI=3∠PMI
∵∠NFH=2∠HFD
∴∠RFN=180°-∠NFH-∠HFD=180°-3∠HFD
∵∠RFN=∠HFD
∴∠PRF=∠FNP+∠RFN=∠FNP+180°-3∠RFM
∴∠MON+∠PRF+∠RFM=360°-∠OMF
即3∠PMI+∠FNP+180°-3∠RFM+∠RFM=360°-∠OMF
∴∠FNP+2∠PMI-2∠RFM=180°-∠PMH
∵3∠PMI+∠PNH=180°
∴3∠PMI+∠FNP+∠FNH=180°
∵3∠RFM+∠FNH=180°
∴3∠PMI-3∠RFM+∠FNP=0°
即∠RFM-∠PMI=![]() ∠FNP
∠FNP
∴∠FNP+2∠PMI-2∠RFM=∠FNP-2(∠RFM-∠PMI)=180°-∠PMH
∠FNP-2×![]() ∠FNP=180°-∠PMH
∠FNP=180°-∠PMH
![]() ∠FNP=180°-∠PMH
∠FNP=180°-∠PMH
即![]() ∠N+∠PMH=180°
∠N+∠PMH=180°
故答案为![]() ∠N+∠PMH=180°
∠N+∠PMH=180°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0),

(1)请直接写出点A关于原点O对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,求出A′点的坐标。
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有四张正面分别标有数字2,1,﹣3,﹣4的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上,洗匀后从四张卡片中随机地摸取一张不放回,将该卡片上的数字记为m,再随机地摸取一张,将卡片上的数字记为n.
(1)请画出树状图并写出(m,n)所有可能的结果;
(2)求所选出的m,n能使一次函数y=mx+n的图象经过第二、三、四象限的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某海域有A,B,C三艘船正在捕鱼作业,C船突然出现故障,向A,B两船发出紧急求救信号,此时B船位于A船的北偏西72°方向,距A船24海里的海域,C船位于A船的北偏东33°方向,同时又位于B船的北偏东78°方向.
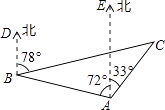
(1)求∠ABC的度数;
(2)A船以每小时30海里的速度前去救援,问多长时间能到出事地点.(结果精确到0.01小时).
(参考数据: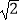 ≈1.414,
≈1.414, 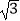 ≈1.732)
≈1.732) -
科目: 来源: 题型:
查看答案和解析>>【题目】京广高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的
 ;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为8.4万元,乙队每天的施工费用为5.6万元.工程预算的施工费用为500万元.为缩短工期并高效完成工程,拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出你的判断并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形ABCD中,∠BAD=60°.
(1)如图1,点E为线段AB的中点,连接DE,CE,若AB=4,求线段EC的长;
(2)如图2,M为线段AC上一点(M不与A,C重合),以AM为边,构造如图所示等边三角形AMN,线段MN与AD交于点G,连接NC,DM,Q为线段NC的中点,连接DQ,MQ,求证:DM=2DQ.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点
 的坐标满足:
的坐标满足:
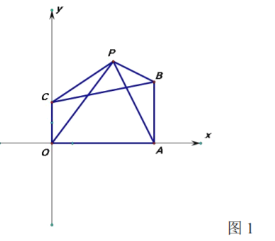
(1)求出点
 的坐标
的坐标(2)如图1,连接
 ,点
,点 在四边形
在四边形 外面且在第一象限,再连
外面且在第一象限,再连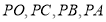 ,则
,则 ,求
,求 点坐标.
点坐标.(3)如图2所示,
 为线段
为线段 上一动点,
上一动点, (在
(在 右侧)为
右侧)为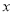 上一动点,使
上一动点,使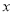 轴始终平分
轴始终平分 ,连
,连 且
且 ,那么
,那么 是否为定值?若为定值,请直接写出定值,若不是,请简单说明理由.
是否为定值?若为定值,请直接写出定值,若不是,请简单说明理由.
相关试题

