【题目】某商店用 500 元购进 A、B 两种铅笔盒共 50 个,这两种铅笔盒的进价、标价如下表所示.
类型 价格 | A 型 | B 型 |
进价(元/个) | 8 | 13 |
标价(元/个) | 12 | 20 |
(1)这两种笔记本各购进多少个?
(2)若 A 型笔记本按标价的 9 折出售,B 型笔记本按标价的 8 折出售,那么这批笔记本 全部售出后,商店共获利多少元?
参考答案:
【答案】(1)购进A型铅笔盒30个,B型铅笔盒20个 (2)144
【解析】
(1)设购进A型铅笔盒x个,B型铅笔盒50-x个,根据题意列方程求解即可.
(2)根据利润公式求解即可.
(1)设购进A型铅笔盒x个,B型铅笔盒50-x个,由题意得
![]()
![]()
![]()
解得![]()
故![]()
故购进A型铅笔盒30个,B型铅笔盒20个.
(2)![]()
![]()
![]()
![]() (元)
(元)
故这批笔记本全部售出后,商店共获利144元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABOC的顶点O在坐标原点,顶点B,C分别在x,y轴的正半轴上,顶点A在反比例函数y=
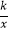 (k为常数,k>0,x>0)的图象上,将矩形ABOC绕点A按逆时针反向旋转90°得到矩形AB′O′C′,若点O的对应点O′恰好落在此反比例函数图象上,则
(k为常数,k>0,x>0)的图象上,将矩形ABOC绕点A按逆时针反向旋转90°得到矩形AB′O′C′,若点O的对应点O′恰好落在此反比例函数图象上,则  的值是 .
的值是 . 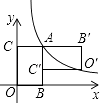
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们来定义下面两种数:
(一)平方和数:若一个三位数或者三位以上的整数分拆成最左边、中间、最右边三个数后满足:中间数=(最左边数)2+(最右边数)2,我们就称该整数为平方和数.
例如:对于整数251.它中间的数字是5,最左边数是2,最右边数是1.
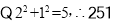 是一个平方和数
是一个平方和数又例如:对于整数3254,它的中间数是25,最左边数是3,最右边数是4,
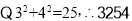 是一个平方和数.当然152和4253这两个数也是平方和数;
是一个平方和数.当然152和4253这两个数也是平方和数;(二)双倍积数:若一个三位数或者三位以上的整数分拆成最左边、中间、最右边三个数后满足:中间数=
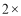 最左边数
最左边数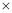 最右边数,我们就称该整数为双倍积数.
最右边数,我们就称该整数为双倍积数.例如:对于整数163,它的中间数是6,最左边数是1,最右边数是3,
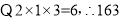 是一个双倍积数,
是一个双倍积数,又例如:对于整数3305,它的中间数是30,最左边数是3,最右边数是5,
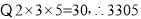 是一个双倍积数,当然361和5303这两个数也是双倍积数.
是一个双倍积数,当然361和5303这两个数也是双倍积数.注意:在下面的问题中,我们统一用字母
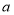 表示一个整数分拆出来的最左边数,用字母
表示一个整数分拆出来的最左边数,用字母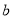 表示该整数分拆出来的最右边数,请根据上述定义完成下面问题:
表示该整数分拆出来的最右边数,请根据上述定义完成下面问题:(1)①若一个三位整数为平方和数,且十位数为4,则该三位数为________;
②若一个三位整数为双倍积数,且十位数字为 6 ,则该三位数为_________;
③若一个整数既为平方和数,又是双倍积数,则
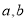 应满足的数量关系为_______;
应满足的数量关系为_______;(2)若
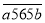 (即这是个最左边数为
(即这是个最左边数为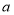 ,中间数为565,最右边数为
,中间数为565,最右边数为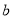 的整数,以下类同)是一个平方和数,
的整数,以下类同)是一个平方和数,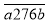 是一个双倍积数,求
是一个双倍积数,求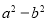 的值.
的值.(3)从所有三位整数中任选一个数为双倍积数的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在矩形
 中,AB=30cm,BC=60cm.点
中,AB=30cm,BC=60cm.点 从点
从点 出发,沿
出发,沿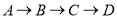 路线向点
路线向点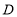 匀速运动,到达点
匀速运动,到达点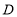 后停止;点
后停止;点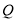 从点
从点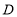 出发,沿
出发,沿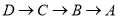 路线向点
路线向点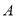 匀速运动,到达点
匀速运动,到达点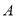 后停止.若点
后停止.若点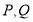 同时出发,在运动过程中,
同时出发,在运动过程中,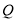 点停留了
点停留了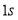 ,图②是
,图②是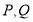 两点在折线
两点在折线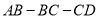 上相距的路程S(cm)与时间
上相距的路程S(cm)与时间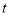 (s)之间的部分函数关系图象.求:
(s)之间的部分函数关系图象.求:(1)P、Q两点的运动速度及P到C点的时间;
(2)设
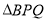 的面积为
的面积为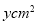 ,求
,求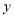 与
与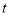 之间的关系式.
之间的关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的有( )
①绝对值等于本身的数是正数;②将数60340精确到千位是
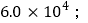 ③连接两点的线段的长度就是两点间的距离;④若AC=BC,则点C就是线段AB的中点.
③连接两点的线段的长度就是两点间的距离;④若AC=BC,则点C就是线段AB的中点.A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
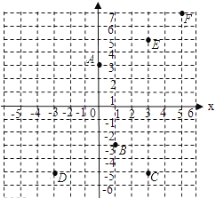
查看答案和解析>>【题目】在平面直角坐标中表示下面各点:A(0,3),B(1,﹣3),C(3,﹣5),D(﹣3,﹣5),E(3,5),F(5,7).
①A点到原点O的距离是________ .
②将点C向x轴的负方向平移6个单位它与点________重合.
③连接CE,则直线CE与y轴位置关系是________ .
④点F分别到x、y轴的距离分别是________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】由太原开往运城的D5303次列车,途中有6个停车站,这次列车的不同票价最多有( )
A. 28种 B. 15种 C. 56种 D. 30种
相关试题

