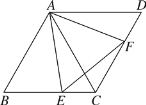
【题目】如图,△ABC和△ACD均为等边三角形,E是BC上的一个动点,F是CD上的一个动点,且∠EAF=60°.
(1)请判断△AEF的形状,并说明理由;
(2)当AB=4时,求△AEF面积的最小值.
参考答案:
【答案】(1)见解析;(2)3![]() .
.
【解析】(1)由等边三角形的性质得到AD=AC,∠D=∠ACB=60°,∠BAC=∠CAD=60°.再由∠EAF=60°,得到∠EAC=∠FAD.即可证明△AEC≌△AFD,由全等三角形的性质得到AE=AF,即可得到△AEF是等边三角形.
(2)由△AEF为等边三角形,得到S△AEF=![]() AE2.要使S△AEF最小,则需使AE最小,当AE⊥BC时,AE最小.求出AE的最小值,代入计算即可.
AE2.要使S△AEF最小,则需使AE最小,当AE⊥BC时,AE最小.求出AE的最小值,代入计算即可.
(1)△AEF是等边三角形.理由如下:
∵△ABC和△ACD均为等边三角形,∴AD=AC,∠D=∠ACB=60°,∠BAC=∠CAD=60°.
又∵∠EAF=60°,∴∠EAC=∠FAD.在△AEC与△AFD中,∵∠EAC=∠FAD,AC=AD,∠ACE=∠D,∴△AEC≌△AFD(ASA),∴AE=AF.
又∵∠EAF=60°,∴△AEF是等边三角形.
(2)由(1)知△AEF为等边三角形,∴S△AEF=![]() AE2.要使S△AEF最小,则需使AE最小,当AE⊥BC时,AE最小.此时.在Rt△ABE中,∵AB=4,∠B=60°,∴∠BAE=30°,∴BE=
AE2.要使S△AEF最小,则需使AE最小,当AE⊥BC时,AE最小.此时.在Rt△ABE中,∵AB=4,∠B=60°,∴∠BAE=30°,∴BE=![]() AB=2,∴AE=
AB=2,∴AE=![]() .∴S△AEF的最小值为
.∴S△AEF的最小值为![]() ×(
×(![]() )2=
)2=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+4交x轴于点A,交y轴于点C,抛物线y=ax2﹣
x+4交x轴于点A,交y轴于点C,抛物线y=ax2﹣  x+c过点A,交y轴于点B(0,﹣2)
x+c过点A,交y轴于点B(0,﹣2)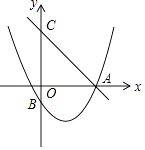
(1)求抛物线的解析式;
(2)点M为抛物线在第四象限部分上的一个动点,求四边形BMAC面积的最大值;
(3)点D为抛物线对称轴上一点,规定:d=|AD﹣BD|,探究d是否存在最大值?若存在,请直接写出d的最大值及此时点D的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】与图中的三角形相似的是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
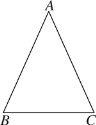
查看答案和解析>>【题目】如图,在△ABC中,AB=AC.
(1)作△ABC的角平分线AD(尺规作图,保留痕迹);
(2)在AD的延长线上任取一点E,连接BE,CE.
①求证:△BDE≌△CDE;
②当AE=2AD时,四边形ABEC是平行四边形吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在江苏卫视《最强大脑》节目中,搭载百度大脑的小度机器人以3:1的总战绩,斩获2017年度脑王巅峰对决的晋级资格,人工智能时代已经扑面而来.
某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进机器人多少个?
(2)若所有机器人都按相同的标价销售,要求全部销售完毕的利润率不低于20%(不考虑其它因素),那么每个机器人的标价至少是多少元?

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
请解决下列问题:
(1)已知点M,N是线段AB的勾股分割点,且BN>MN>AM.若AM=2,MN=3,求BN的长;
(2)如图2,若点F、M、N、G分别是AB、AD、AE、AC边上的中点,点D,E是线段BC的勾股分割点,且EC>DE>BD,求证:点M,N是线段FG的勾股分割点.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)如图,在等腰直角三角形MNC中,CN=MN=
 ,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.
,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.(1)∠NCO的度数为________;
(2)求证:△CAM为等边三角形;
(3)连接AN,求线段AN的长.

相关试题

