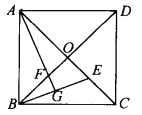
【题目】(满分8分)如图,正方形ABCD中对角线AC、BD相交于O,E为AC上一点,AG⊥EB交EB于G,AG交BD于F.
(1)说明OE=OF的道理;
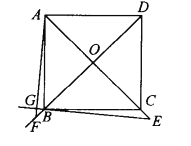
(2)在(1)中,若E为AC延长线上,AG⊥EB交EB的延长线于G,AG、BD的延长线交于F,其他条件不变,如图2,则结论:“OE=OF”还成立吗?请说明理由.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)根据正方形的性质利用ASA判定△AOF≌△BOE,根据全等三角形的对应边相等得到OE=OF;(2)类比(1)的方法证得同理得出结论成立.
试题解析:(1),在正方形ABCD中,
∴AO=BO,∠AOF=∠BOE=90°,
∴∠OBE+∠BEO=90°,
∵AG⊥EB,
∴∠AGE=90°,
∴∠GAE+∠AEG=90°,
∴∠OBE=∠OAF,
在△AOF和△BOE中,
 ,
,
∴△AOF≌△BOE(ASA),
∴OE=OF.
(2)OE=OF仍然成立。
理由:正方形ABCD中,∴AO=BO,∠AOF=∠BOE=90°,
∴∠FAO+∠F=90°,
∵AG⊥EB,∴∠AGE=90°,
∴∠GAE+∠E=90°,
∴∠E=∠F,
在△AOF和△BOE中,
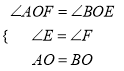 ,
,
∴△AOF≌△BOE(AAS),
∴OE=OF.
所以结论仍然成立。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,不是多项式2x2﹣4x+2的因式的是( )
A. 2B. 2(x﹣1)C. (x﹣1)2D. 2(x﹣2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=﹣2是关于x的一元二次方程x2+3x+m+1=0的一个解,则m= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:x2+6x﹣7=0.
-
科目: 来源: 题型:
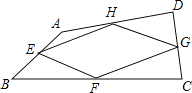
查看答案和解析>>【题目】(满分8分)我们把依次连接任意四边形各边中点得到的四边形叫做中点四边形.
如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,依次连接各边中点得到中点四边形EFGH.
(1)这个中点四边形EFGH的形状是____________;
(2)证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛硬币15次,有6次出现正面,9次出现反面,则出现正面的频数是( )
A.6
B.9
C.15
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】某市一天上午的气温是10 ℃,下午上升了2 ℃,半夜(24时)下降了15 ℃,则半夜的气温是( )
A. 3 ℃ B. -3 ℃ C. 4 ℃ D. -2 ℃
相关试题

