【题目】如图,在平面直角坐标系中, ![]() 为坐标原点,直线
为坐标原点,直线 ![]() :
: ![]() 与直线
与直线 ![]() :
: ![]() 交于点
交于点 ![]() ,
, ![]() 与
与 ![]() 轴交于
轴交于 ![]() ,与
,与 ![]() 轴交于点
轴交于点 ![]() .
.
(1)求 ![]() 的面积;
的面积;
(2)若点 ![]() 在直线
在直线 ![]() 上,且使得
上,且使得 ![]() 的面积是
的面积是 ![]() 面积的
面积的 ![]() ,求点
,求点 ![]() 的坐标.
的坐标.
参考答案:
【答案】
(1)解:由 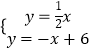 得:
得: ![]()
∴A(4,2)
在y=-x+6中,当x=0,y=6,则C(0,6),S△OAC= ![]() ×6×4=12
×6×4=12
(2)解:解:分两种情况:①如图所示,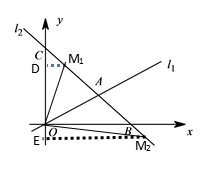
当点M1在射线AC上时,过M1作M1D⊥CO于D,则△CDM1是等腰直角三角形,
∵A(4,2),C(0,6),
∴AC= ![]() =4
=4![]() ,
,
∵△OAM的面积是△OAC面积的![]() ,
,
∴AM1=![]() AC=3
AC=3![]() ,
,
∴CM1= ![]() ,
,
∴DM1= ![]() ,即点M1的横坐标为
,即点M1的横坐标为 ![]() ,
,
在直线y=﹣x+6中,当x=![]() 时,y=6﹣
时,y=6﹣ ![]() ,
,
∴M1(![]() ,6﹣
,6﹣ ![]() );
);
②如图所示,当点M2在射线AB上时,过M2作M2E⊥CO于E,则△CEM2是等腰直角三角形,
由题可得,AM2=AM1=3![]() ,
,
∴CM2=7 ![]() ,
,
∴EM2= ![]() ,即点M2的横坐标为
,即点M2的横坐标为![]() ,
,
在直线y=﹣x+6中,当x= ![]() 时,y=6﹣
时,y=6﹣ ![]() ,
,
∴M2( ![]() ,6﹣
,6﹣ ![]() ).
).
综上所述,点M的坐标为(![]() ,6﹣
,6﹣![]() )或(
)或( ![]() ,6﹣
,6﹣ ![]() ).
).
【解析】(1)先求出两直线的交点A的坐标,及直线BC与y轴的交点C的坐标,再根据三角形的面积公式,即可求出△OAC的面积。
(2)抓住已知条件中的关键词点M在直线l2上,因此分两种情况讨论:当点M1在射线AC上时,过M1作M1D⊥CO于D,则△CDM1是等腰直角三角形,易求出AC的长,再根据△OAM和△OAC的面积关系求出AM1,CM1的长,由△CDM1是等腰直角三角形,可得出DM1的长,然后结合函数解析式就可求出 点M1的坐标;当点M2在射线AB上时,过M2作M2E⊥CO于E,则△CEM2是等腰直角三角形,运用类似的方法求出点M2的坐标,即可得出结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列不能运用平方差公式运算的是( )
A. (a+b)(b+a)B. (a+b)(ab)C. (a+b)(ab)D. (ab)(ab)
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用二元一次方程组解应用题:甲、乙两地相距
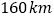 ,一辆汽车和一辆拖拉机同时由两地以各自的速度匀速相向而行,
,一辆汽车和一辆拖拉机同时由两地以各自的速度匀速相向而行, 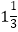 小时后相遇.相遇后,拖拉机以其原速继续前进,汽车在相遇处停留
小时后相遇.相遇后,拖拉机以其原速继续前进,汽车在相遇处停留 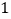 小时后调转车头以其原速返回,在汽车再次出发半小时追上拖拉机.这时,汽车、拖拉机各自走了多少路程?
小时后调转车头以其原速返回,在汽车再次出发半小时追上拖拉机.这时,汽车、拖拉机各自走了多少路程? -
科目: 来源: 题型:
查看答案和解析>>【题目】若x2+4x﹣4=0,则2x2+8x+7的值等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如右图,
 为等腰
为等腰 的外接圆,直径
的外接圆,直径 ,
, 为弧
为弧 上任意一点(不与
上任意一点(不与 ,
, 重合),直线
重合),直线 交
交 延长线于点
延长线于点 ,
, 在点
在点 处切线
处切线 交
交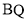 于点
于点 ,下列结论正确的是 .(写出所有正确结论的序号)
,下列结论正确的是 .(写出所有正确结论的序号)①若
 ,则弧
,则弧 的长为
的长为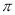 ; ②若
; ②若 ,则
,则 平分
平分 ;
;③若
 ,则
,则 ; ④无论点
; ④无论点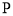 在弧
在弧 上的位置如何变化,
上的位置如何变化, 为定值.
为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)
如图,抛物线
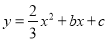 经过点
经过点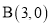 ,
,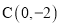 ,直线
,直线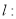
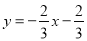 交
交 轴于点
轴于点 ,且与抛物线交于
,且与抛物线交于 ,
, 两点.
两点. 为抛物线上一动点(不与
为抛物线上一动点(不与 ,
, 重合).
重合).(1)求抛物线的解析式;
(2)当点
 在直线
在直线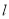 下方时,过点
下方时,过点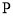 作
作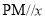 轴交
轴交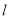 于点
于点 ,
, 轴交
轴交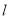 于点
于点 .求
.求 的最大值;
的最大值;(3)设
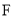 为直线
为直线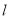 上的点,以
上的点,以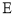 ,
, ,
,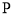 ,
,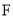 为顶点的四边形能否构成平行四边形?若能,求出点
为顶点的四边形能否构成平行四边形?若能,求出点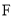 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.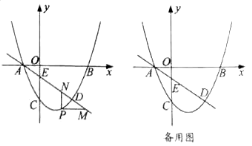
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:m8÷m3=____.
相关试题

