搜索
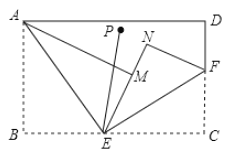
【题目】如图，将一张长方形的纸片分别沿
、
折叠后，点
落在点
处，点
落在点
处，且
、、三点刚好在同一直线上，折痕分别为、，射线
为
的角平分线，则下列说法中：①是
的平分线；②
是
的平分线；③
；④
．其中正确的有（ ）
A.1个B.2个C.3个D.4个
参考答案：
【答案】C
【解析】
根据矩形的性质，翻折变换解决问题即可．
解：由翻折可知：AE是∠MAB的角平分线，故①正确，
无法判断AM平分∠DAE，故②错误，
由翻折可知：∠AEM＝
∠BEM，∠FEN＝∠CEN，
∴∠AEM+∠FEN＝（∠BEM+∠CEN）＝90°，
∴∠AEF＝90°，
∵EP平分∠AEF，
∴∠AEP＝×90°＝45°，故④正确，
∵BE＝EM，EC＝EN，
∴ME+EN＝BE+EC＝BC，故③正确，
故选：C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】有三张正面分别标有数字：-1，1，2的卡片，它们除数字不同外其余全部相同，现将它们背面朝上，洗匀后从中随机抽出一张记下数字，放回洗匀后再从中随机抽出一张记下数字．
(1)请用列表或画树形图的方法（只选其中一种），表示两次抽出卡片上的数字的所有结果；
(2)将第一次抽出的数字作为点的横坐标x，第二次抽出的数字作为点的纵坐标y，求点（x，y）落在双曲线
上的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】某校九年级举行毕业典礼，需要从九（1）班的2名男生1名女生、九（2）的1名男生1名女生共5人中选出2名主持人．
（1）用树形图或列表法列出所有可能情形；
（2）求2名主持人来自不同班级的概率；
（3）求2名主持人恰好1男1女的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了加强学生的交通安全意识，某中学和交警大队联合举行了“我当一日小交警”活动，星期天选派部分学生到交通路口值勤，协助交通警察维护交通秩序．若每一个路口安排4人，那么还剩下78人；若每个路口安排8人，那么最后一个路口不足8人，但不少于4人．求这个中学共选派值勤学生多少人？共有多少个交通路口安排值勤？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商场为了吸引顾客，设计了一种促销活动：在一个不透明的箱子里放有4个相同的小球，球上分别标有“0元”、“10元”、“20元”和“30元”的字样．规定：顾客在本商场同一日内，每消费满200元，就可以在箱子里先后摸出两个球（第一次摸出后不放回），商场根据两小球所标金额的和返还相应价格的购物券，可以重新在本商场消费，某顾客刚好消费200元．
（1）该顾客至少可得到_____元购物券，至多可得到_______元购物券；
（2）请你用画树状图或列表的方法，求出该顾客所获得购物券的金额不低于30元的概率．
-
科目： 来源： 题型：
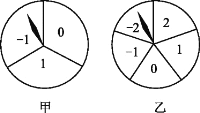
查看答案和解析>>【题目】如图,有甲、乙两个可以自由转动的转盘,其中转盘甲被平均分成三个扇形,转盘乙被平均分成五个扇形.小明与小亮玩转盘游戏,规则如下:同时转动两个转盘,转盘停止后,转盘甲指针所指数字作为点的横坐标,转盘乙指针所指数字作为点的纵坐标(当指针指在边界线时视为无效,重转),从而确定一个点的坐标为A(m,n).当点A在第一象限时,小明赢;当点A在第二象限时,小亮赢.请你利用画树状图或列表法分析该游戏规则对双方是否公平?并说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商店购进600个旅游纪念品，进价为每个6元，第一周以每个10元的价格售出200个，第二周若按每个10元的价格销售仍可售出200个，但商店为了适当增加销量，决定降价销售（根据市场调查，单价每降低1元，可多售出50个，但售价不得低于进价），单价降低x元销售销售一周后，商店对剩余旅游纪念品清仓处理，以每个4元的价格全部售出，如果这批旅游纪念品共获利1250元，问第二周每个旅游纪念品的销售价格为多少元？
相关试题
