【题目】如图,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q.
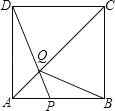
(1)试证明:无论点P运动到AB上何处时,都有△ADQ≌△ABQ;
(2)若点P从点A运动到点B,再继续在BC上运动到点C,在整个运动过程中,当点P 运动到什么位置时,△ADQ恰为等腰三角形.
参考答案:
【答案】(1)证明见解析;(2)当点P运动到①点B的位置;②在BC上,且到点B的距离为8﹣4![]() 处;③运动到点C的位置时,△ADQ恰为等腰三角形.
处;③运动到点C的位置时,△ADQ恰为等腰三角形.
【解析】
试题分析:(1)根据正方形的四条边都相等可得AD=AB,对角线平分一组对角可得∠DAQ=∠BAQ=45°,然后利用“边角边”证明△ADQ和△ABQ全等;
(2)分①AQ=DQ时,点B、P重合,②AQ=AD时,根据等边对等角可得∠ADQ=∠AQD,再求出正方形的对角线AC的长,再求出CQ,然后根根据两直线平行,内错角相等求出∠CPQ=∠ADQ,从而得到∠CQP=∠CPQ,根据等角对等边可得CP=CQ,从而得到点P的位置,③AD=DQ时,点C、P、Q三点重合.
(1)证明:在正方形ABCD中,无论点P运动到AB上何处时,
都有AD=AB,∠DAQ=∠BAQ=45°,
在△ADQ和△ABQ中,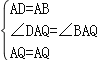 ,
,
∴△ADQ≌△ABQ(SAS);
(2)若△ADQ是等腰三角形,
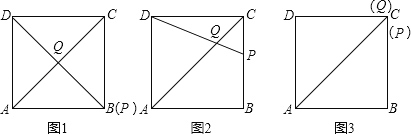
则有①如图1,AQ=DQ时,点Q为正方形ABCD的中心,点B、P重合;
②如图2,AQ=AD时,根据等边对等角有∠ADQ=∠AQD,
∵正方形ABCD的边长为4,
∴AC=![]() =4
=4![]() ,
,
∴CQ=AC﹣AQ=4![]() ﹣4,
﹣4,
∵AD∥BC,
∴∠CPQ=∠ADQ,
∴∠CQP=∠CPQ,
∴CP=CQ=4![]() ﹣4,
﹣4,
此时点P在距离点B:4﹣(4![]() ﹣4)=8﹣4
﹣4)=8﹣4![]() ;
;
③如图3,AD=DQ时,点C、P、Q三点重合;
综上所述,当点P运动到①点B的位置;②在BC上,且到点B的距离为8﹣4![]() 处;③运动到点C的位置时,△ADQ恰为等腰三角形.
处;③运动到点C的位置时,△ADQ恰为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一元二次方程x2﹣2x﹣a=0没有实数根,则一次函数y=(a+1)x+(a﹣1)的图象不过第( )
A.一象限 B.二象限 C.三象限 D.四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】若某地打长途电话3分钟之内收费1.8元,3分钟以后每增加1分钟(不到1分钟按1分钟计算)加收0.5元,当通话时间t≥3分钟时,电话费y(元)与通话时间t(分)之间的关系式为___________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
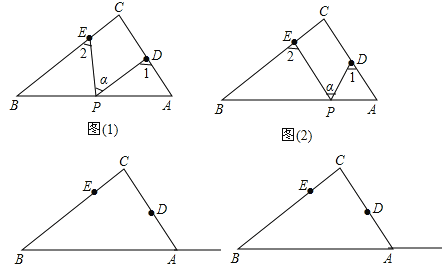
(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2= °;
(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间有何关系?说明理由.
(3)若点P在Rt△ABC斜边BA的延长线上运动(CE<CD),则∠α、∠1、∠2之间有何关系?猜想并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x2+kx+25是一个完全平方式,则k=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各点,在一次函数y=2x+6的图象上的是( )
A. (-5,4) B. (-4,1) C. (4,20) D. (-3, 0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,有一Rt△ABC,且A(﹣1,3),B(﹣3,﹣1),C(﹣3,3),已知△A1AC1是由△ABC旋转得到的.
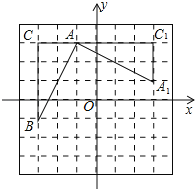
(1)请写出旋转中心的坐标是 ,旋转角是 度;
(2)以(1)中的旋转中心为中心,画出△A1AC1顺时针旋转90°的三角形.
相关试题

