【题目】某服装厂现有甲种布料42米,乙种布料30米.现计划用这两种布料生产M,N两种型号的校服共40件,已知做一件M型号的校服需要用甲种布料0.8米,乙种布料1.1米.做一件N型号的校服需用甲种布料1.2米,乙种布料0.5米,按要求生产M,N两种型号的校服,有哪几种生产方案?请你设计出来.
参考答案:
【答案】解:设要做x件N型号的校服,则需做(40﹣x)件M型号的校服,
由题意得: ![]() ,解得:
,解得: ![]() .
.
所以有两种方案.
方案一:生产M型号的校服15件,N型号的校服25件;
方案二:生产M型号的校服16件,N型号的校服24件.
【解析】关系式为:M型号的校服件数×0.8+N型号的校服件数×1.2≤42;M型号的校服件数×1.1+N型号的校服件数×0.5≤30.
【考点精析】本题主要考查了一元一次不等式组的应用的相关知识点,需要掌握1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了迎接校运会开幕式,现要求甲乙两队赶制小红旗,已知甲队的工作效率是乙队的2倍,若两队各单独赶制400面小红旗,甲队比乙队少用4天完成.
(1)问甲、乙两队每天各能制作多少面小红旗?
(2)已知甲队、乙队每天的制作费用分别是400元、250元,若要制作的小红旗的数量为1800面,且总费用不超过8000元,问至少应安排甲队制作多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若32×2n=29,则n=____.若8×23×32×(-2)8=2x,则x=____
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知am=3,an=4,化简下列各式:(1)am+1=______; (2)a3+n=_______; (3)am+n+2=_______.
-
科目: 来源: 题型:
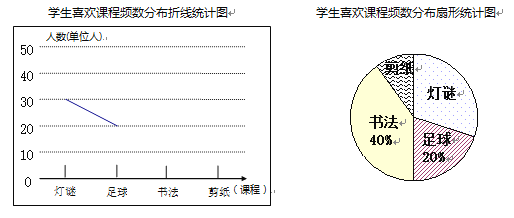
查看答案和解析>>【题目】某校校本课程中心为了解该校学生喜欢校本课程的情况,采取抽样调查的办法,通过书法、剪纸、灯谜、足球四门课程的选报情况调查若干名学生的兴趣爱好,要求每位同学只能选择一门自己喜欢的课程,并将调查结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息,解答:
(1)在这次调查研究中,一共调查了______名学生;
(2)喜欢剪纸的人数在扇形统计图中所占的圆心角是多少度?请补全频数分布折线统计图;
(3)为了平衡各校本课程的人数,需要从喜欢书法课程的甲、乙、丙3人中调整2人到剪纸课程,求“甲乙两人被同时调整到剪纸课程”的概率,试用画树状图或列表说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司销售部有五名销售员,2007年平均每人每月的销售额分别是6,8,11,9,8(万元),现公司需增加一名销售员,三人应聘试用三个月,平均每人每月的销售额分别为:甲是上述数据的平均数,乙是中位数,丙是众数,最后录用三人中平均月销售额最高的人是___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)10m×10 000=_________; (2)3n-4×(-3)3×35-n=__________.
相关试题

