【题目】如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)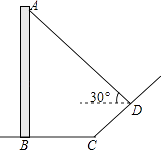
参考答案:
【答案】解:延长AD交BC的延长线于E,作DF⊥BE于F,
∵∠BCD=150°,
∴∠DCF=30°,又CD=4,
∴DF=2,CF= ![]() =2
=2 ![]() ,
,
由题意得∠E=30°,
∴EF= ![]() =2
=2 ![]() ,
,
∴BE=BC+CF+EF=6+4 ![]() ,
,
∴AB=BE×tanE=(6+4 ![]() )×
)× ![]() =(2
=(2 ![]() +4)米,
+4)米,
答:电线杆的高度为(2 ![]() +4)米.
+4)米.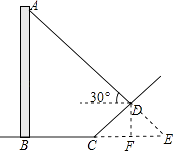
【解析】延长AD交BC的延长线于E,作DF⊥BE于F,根据直角三角形的性质和勾股定理求出DF、CF的长,根据正切的定义求出EF,得到BE的长,根据正切的定义解答即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两组同学进行一分钟引体向上测试,评分标准规定,做6个以上
 含6个
含6个 为合格,做9个以上
为合格,做9个以上 含9个
含9个 为优秀,两组同学的测试成绩如下表:
为优秀,两组同学的测试成绩如下表:成绩
 个
个
4
5
6
7
8
9
甲组
 人
人
1
2
5
2
1
4
乙组
 人
人
1
1
4
5
2
2
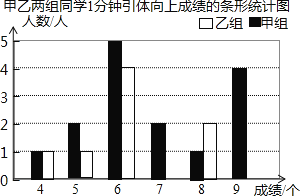
现将两组同学的测试成绩绘制成如下不完整的统计图表:
统计量
平均数
 个
个
中位数
众数
方差
合格率
优秀率
甲组
a
6
6



乙组
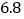
b
7



 将条形统计图补充完整;
将条形统计图补充完整; 统计表中的
统计表中的 ______,
______,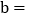 ______;
______; 人说甲组的优秀率高于乙组优秀率,所以甲组成绩比乙组成绩好,但也有人说乙组成绩比甲组成绩好,请你给出两条支持乙组成绩好的理由.
人说甲组的优秀率高于乙组优秀率,所以甲组成绩比乙组成绩好,但也有人说乙组成绩比甲组成绩好,请你给出两条支持乙组成绩好的理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
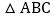 中,
中,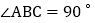 ,BD为AC边上的中线,过点C作
,BD为AC边上的中线,过点C作 于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取
于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取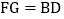 ,连接BG,DF.
,连接BG,DF. 求证:
求证: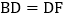 ;
; 求证:四边形BDFG为菱形;
求证:四边形BDFG为菱形; 若
若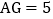 ,
,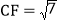 ,求四边形BDFG的周长.
,求四边形BDFG的周长.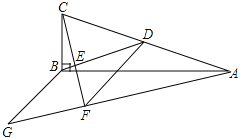
-
科目: 来源: 题型:
查看答案和解析>>【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展,据调查,某家快递公司,今年三月份与五月份完成投递的快件总件数分别是5万件和
 万件,现假定该公司每月投递的快件总件数的增长率相同.
万件,现假定该公司每月投递的快件总件数的增长率相同. 求该公司投递快件总件数的月平均增长率;
求该公司投递快件总件数的月平均增长率; 如果平均每人每月可投递快递
如果平均每人每月可投递快递 万件,那么该公司现有的16名快递投递员能否完成今年6月份的快递投递任务?
万件,那么该公司现有的16名快递投递员能否完成今年6月份的快递投递任务? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D.
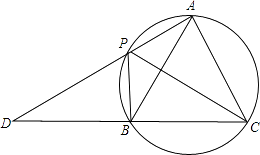
(1)求证:△ABC是等边三角形;
(2)若∠PAC=90°,AB=2 ,求PD的长.
,求PD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆有客房50间,当每间客房每天的定价为220元时,客房会全部住满;当每间客房每天的定价增加10元时,就会有一间客房空闲,设每间客房每天的定价增加x元时,客房入住数为y间.
(1)求y与x的函数关系式(不要求写出x的取值范围);
(2)如果每间客房入住后每天的各种支出为40元,不考虑其他因素,则该宾馆每间客房每天的定价为多少时利润最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,需在一面墙上绘制几个相同的抛物线型图案.按照图中的直角坐标系,最左边的抛物线可以用y=ax2+bx(a≠0)表示.已知抛物线上B,C两点到地面的距离均为
 m,到墙边OA的距离分别为
m,到墙边OA的距离分别为  m,
m,  m.
m. 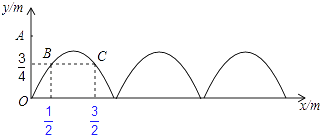
(1)求该拋物线的函数关系式,并求图案最高点到地面的距离;
(2)若该墙的长度为10m,则最多可以连续绘制几个这样的拋物线型图案?
相关试题

