【题目】如图,在建立平面直角坐标系的网格纸中,每个小方格都是边长为1个单位长度的小正方形,△ABC的顶点均在格点上,点P的坐标为(-1,0).
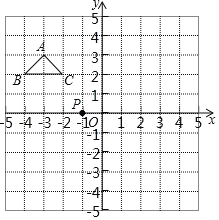
(1)把△ABC绕点P旋转180°得到△A’B’C’,作出△A’B’C’;
(2)把△ABC向右平移7个单位长度得到△A″B″C″,作出△A″B″C″;
(3)△A’B’C’与△A″B″C″是否成中心对称?若是,则找出对称中心P’,并写出其坐标;若不是,请说明理由.
参考答案:
【答案】(1)见解析;(2)见解析;(3)P'(2.5,0)
【解析】
(1)根据网格结构找出点A、B、C绕点P旋转180°的对应点A′、B′、C′位置,然后顺次连接即可;
(2)根据网格结构找出点A、B、C平移后的对应点A″、B″、C″的位置,然后顺次连接即可;
(3)利用观察对应点的连线即可求解.
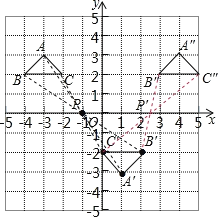
解:(1)如图,△A'B'C'即为所求;
(2)如图,A'B'C'即为所求;
(3)如图,P'(2.5,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在等腰三角形ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,CE与BD交于点O.

(1)求证:△BCE≌△CBD;
(2)写出图中所有相等的线段.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知Rt△ABC中,∠BAC=90°,AB=AC,点E为△ABC内一点,连接AE,CE,CE⊥AE,过点B作BD⊥AE,交AE的延长线于D.

(1)如图1,求证BD=AE;
(2)如图2,点H为BC中点,分别连接EH,DH,求∠EDH的度数;
(3)如图3,在(2)的条件下,点M为CH上的一点,连接EM,点F为EM的中点,连接FH,过点D作DG⊥FH,交FH的延长线于点G,若GH:FH=6:5,△FHM的面积为30,∠EHB=∠BHG,求线段EH的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解不等式:
 ,并把它的解集表示在数轴上;
,并把它的解集表示在数轴上;(2)解不等式组
 ,并写出它的所有非负整数解.
,并写出它的所有非负整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,直接写出它的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x,y的方程组
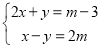 的解,x,y均为负数.
的解,x,y均为负数.(1)求m的取值范围;
(2)化简:|m-5|+|m+1|
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G.

(1)求证:AD垂直平分EF;
(2)若∠BAC=60°,猜测DG与AG间有何数量关系?请说明理由.
相关试题

