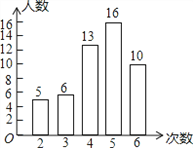
【题目】我市开展了“寻找雷锋足迹”的活动,某中学为了解七年级1000名学生在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题:
(1)所调查的七年级50名学生在这个月内做好事次数的平均数是 ,众数是 ,中位数是 ;
(2)根据样本数据,估计该校七年级1000名学生在“学雷锋活动月”中做好事大于4次的人数.
参考答案:
【答案】(1)4.4,5,5;(2)520
【解析】(1)由条形统计图可得到做好事的次数所对应的人数,那么结合平均数、众数以及中位数的概念即可解决.
(2)根据条形图可得到50名学生做好事不少于4次的人数,那么1000名学生做好事不少于4次的人数即可求得.
(1)平均数;(2×5+3×6+4×13+5×16+6×10)÷50=4.4;
众数:5次; 中位数:5.
(2)做好事大于4次的人数: ![]()
估计该校七年级1000名学生在“学雷锋活动月”中做好事大于4次的人数约为520人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE= 度;
(2)设∠BAC=
 ,∠DCE=
,∠DCE=  .
.① 如图2,当点D在线段CB上,∠BAC≠90°时,请你探究
 与
与 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;② 如图3,当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,并直接写出此时
 与
与 之间的数量关系(不需证明).
之间的数量关系(不需证明).
-
科目: 来源: 题型:
查看答案和解析>>【题目】“绿水青山就是金山银山”,为保护生态环境,某地准备开荒种树,两次参加活动的人数及开支如下表:
开荒(人)
种树(人)
总支出(元)
第一次
15
9
57000
第二次
10
16
68000
(1)若两次开荒种树活动的人均支出费用一样,求开荒和种树的人均支出费用各是多少?
(2)在人均支出费用不变的情况下,为节约开支,施工单位准备抽调40人参加此活动,要使得总支出不超过102 000元,且开荒人数小于种树人数,则有哪几种分配人员方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】蚌埠“一带一路”国际龙舟邀请赛期间,小青所在学校组织了一次“龙舟”故事知多少比赛,小青从全体学生中随机抽取部分同学的分数(得分取正整数,满分为100分)进行统计.以下是根据抽取同学的分数制作的不完整的频率分布表和频率分布直方图,请根据图表,回答下列问题: :
组别
分组
频数
频率
1
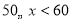
9
0.18
2
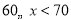
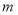
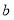
3
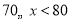
21
0.42
4
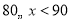
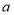
0.06
5
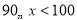
2
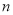

(1)根据上表填空:
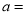 __,
__,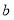 =. ,
=. ,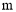 = .
= .(2)若小青的测试成绩是抽取的同学成绩的中位数,那么小青的测试成绩在什么范围内?
(3)若规定:得分在
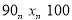 的为“优秀”,若小青所在学校共有600名学生,从本次比赛选取得分为“优秀”的学生参加决赛,请问共有多少名学生被选拔参加决赛?
的为“优秀”,若小青所在学校共有600名学生,从本次比赛选取得分为“优秀”的学生参加决赛,请问共有多少名学生被选拔参加决赛? -
科目: 来源: 题型:
查看答案和解析>>【题目】某同学准备报名参加运动会,有以下4个项目可供选择. 径赛项目:100m,200m (分别用A 、B表示);田赛项目:跳远 ,跳高(分别用C 、D表示).
(1)该同学从4个项目中任选一个,恰好是田赛项目的概率为 ;
(2)该同学从4个项目中任选两个,利用树状图或表格列举出所有可能出现的结果(请用A、B、C、D表示相对应的项目),并求恰好是一个田赛项目和一个径赛项目的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EB.若AB=8,CD=2.
(1) 求⊙O半径OA的长;
(2) 求EB的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1) ,折叠平行四边形
 ,使得
,使得 分别落在
分别落在 边上的
边上的 点,
点, 为折痕
为折痕
(1)若
 ,证明:平行四边形
,证明:平行四边形 是菱形;
是菱形;(2)若
 ,求
,求 的大小;
的大小;(3)如图(2) ,以
 为邻边作平行四边形
为邻边作平行四边形 ,若
,若 ,求
,求 的大小
的大小
相关试题

