【题目】已知抛物线y=ax2+bx+c的图像如图所示,则下列结论:
①abc>0;②a+b+c=2;③b>1;④a< ![]() .
.
其中正确的结论是( )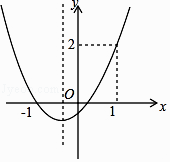
A.①②
B.②③
C.③④
D.②④
参考答案:
【答案】B
【解析】解:①∵抛物线的开口向上,∴a>0,
∵与y轴的交点为在y轴的负半轴上,∴c<0,
∵对称轴为x= ![]() <0,∴a、b同号,即b>0,
<0,∴a、b同号,即b>0,
∴abc<0,
故本选项错误;
②当x=1时,函数值为2,
∴a+b+c=2;
故本选项正确;
③当x=﹣1时,函数值<0,
即a﹣b+c<0,(1)
又a+b+c=2,
将a+c=2﹣b代入(1),
2﹣2b<0,
∴b>1
故本选项正确;
④∵对称轴x=- ![]() >﹣1,
>﹣1,
解得: ![]() <a,
<a,
∵b>1,
∴a> ![]() ,
,
故本选项错误;
综上所述,其中正确的结论是②③;
故选B.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小方格都是边长为1的正方形,已知学校的坐标为A(2,2).
(1)请在图中建立适当的直角坐标系,并写出图书馆的坐标;
(2)若体育馆的坐标为C(-2,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】电力公司为鼓励市民节约用电,采取按月用电量分段收费办法.若某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:
(1) 分别写出当0≤x≤100和x>100时,y与x的函数关系式
(2) 利用函数关系式,说明电力公司采取的收费标准
(3) 若该用户某月用电62度,则应缴费多少元?若该用户某月缴费105元时,则该用户该月用了多少度电?
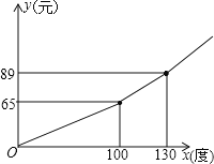
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=-2x+1的图象与y轴交于点A.
(1)若点A关于x轴的对称点B在一次函数y=
 x+b的图象上,求b的值,并在同一坐标系中画出该一次函数的图象;
x+b的图象上,求b的值,并在同一坐标系中画出该一次函数的图象;(2)求这两个一次函数的图象与y轴围成的三角形的面积.
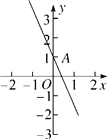
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据国家发改委实施“阶梯电价”的有关文件要求,三明市结合地方实际,决定对居民生活用电试行“阶梯电价”收费,具体收费标准见表:
一户居民一个月用电量的范围
电费价格(单位:元/千瓦时)
不超过150千瓦时
a
超过150千瓦时的部分
b
2017年5月份,居民甲用电100度,交电费80元;居民乙用电190度,交电费160元.
(1)表中,a= ,b= ;
(2)试行“阶梯电价”收费以后,该市一户居民2017年8月份平均电价每度为0.9元,求该用户8月用电多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B、C 为数轴上三点,若点 C 到点 A 的距离是点 C 到点 B 的距离的 2倍,则称点 C 是(A,B)的奇异点,例如图 1 中,点 A 表示的数为﹣1,点B 表示的数为 2,表示 1 的点 C 到点 A 的距离为 2,到点 B 的距离为 1,则点C 是(A,B)的奇异点,但不是(B,A)的奇异点.
(1)在图 1 中,直接说出点 D 是(A,B)还是(B,C)的奇异点;
(2)如图 2,若数轴上 M、N 两点表示的数分别为﹣2 和 4,(M,N)的奇异点 K 在 M、N 两点之间,请求出 K 点表示的数;
(3)如图 3,A、B 在数轴上表示的数分别为﹣20 和 40,现有一点 P 从点 B 出发,向左运动.
①若点 P 到达点 A 停止,则当点 P 表示的数为多少时,P、A、B 中恰有一个点为其余两点的奇异点?
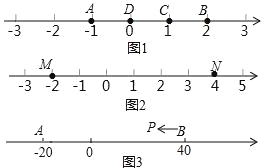
②若点 P 到达点 A 后继续向左运动,是否存在使得 P、A、B 中恰有一个点为其余两点的奇异点的情况?若存在,请直接写出此时 PB 的距离;若不存在,请说明理由.
-
科目: 来源: 题型:
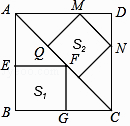
查看答案和解析>>【题目】如图,大正方形ABCD中有2个小正方形,如果它们的面积分别是s1 , s2 , 那么s1s2 . (填>,<或=)
相关试题

