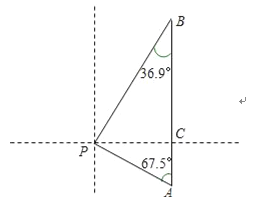
【题目】如图某天上午9时,向阳号轮船位于A处,观测到某港口城市P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到城市P位于该船的南偏西36.9°方向,求此时轮船所处位置B与城市P的距离?(参考数据:sin36.9°≈![]() ,tan36.9°≈
,tan36.9°≈![]() ,sin67.5°≈
,sin67.5°≈![]() ,tan67.5°≈
,tan67.5°≈![]() )
)
参考答案:
【答案】向阳号轮船所处位置B与城市P的距离为100海里.
【解析】
试题分析:首先根据题意可得PC⊥AB,然后设PC=x海里,分别在Rt△APC中与Rt△PCB中,利用正切函数求得出AC与BC的长,由AB=21×5,即可得方程,解此方程即可求得x的值,继而求得答案.
试题解析:根据题意得:PC⊥AB,
设PC=x海里.
在Rt△APC中,∵tan∠A=![]() ,
,
∴AC=![]() ,
,
在Rt△PCB中,∵tan∠B=![]() ,
,
∴BC=![]()
∵AC+BC=AB=21×5,
∴![]() =21×5,
=21×5,
解得x=60.
∵sin∠B=![]() ,
,
∴PB=![]() =60×
=60×![]() =100(海里).
=100(海里).
∴向阳号轮船所处位置B与城市P的距离为100海里.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在●〇●〇〇●〇〇〇●〇〇〇〇●〇〇〇〇〇中,空心圈“〇”出现的频率是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等式ax+c=ay+c,则下列等式不一定成立的是( )
A. ax=ay
B. x=y
C. m-ax=m-ay
D. 2ax=2ay
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题①同旁内角互补,两直线平行;②全等三角形的周长相等;③直角都相等;④等边对等角。它们的逆命题是真命题的个数是( )
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一根可伸缩的鱼竿,鱼竿是用10节大小不同的空心套管连接而成.闲置时鱼竿可收缩,完全收缩后,鱼竿长度即为第1节套管的长度(如图1所示):使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示).图3是这跟鱼竿所有套管都处于完全拉伸状态下的平面示意图.已知第1节套管长50cm,第2节套管长46cm,以此类推,每一节套管均比前一节套管少4cm.完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为xcm.
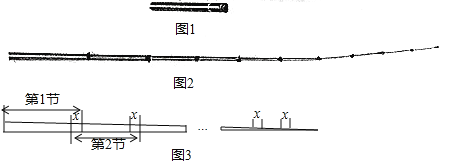
(1)请直接写出第5节套管的长度;
(2)当这根鱼竿完全拉伸时,其长度为311cm,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学开展“阳光体育一小时”活动,根据学校实际情况,决定开设A:踢毽子;B:篮球;C:跳绳;D:乒乓球四种运动项目.为了解学生最喜欢哪一种运动项目,随机抽取了一部分学生进行调查,并将调查结果绘制成如下两个统计图.请结合图中的信息解答下列问题:
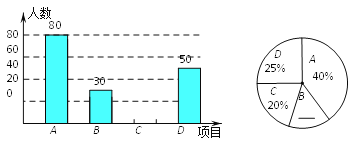
(1)本次共调查了多少名学生?
(2)请将两个统计图补充完整.
(3)若该中学有1200名学生,喜欢篮球运动项目的学生约有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),点
 为线段
为线段 上一点,过点
上一点,过点 作射线
作射线 ,使
,使 ,将一直角三角板的直角顶点放在点
,将一直角三角板的直角顶点放在点 处,一边
处,一边 在射线
在射线 上,另一边
上,另一边 在线段
在线段 的下方.
的下方.(1)将图(1)中的直角三角板绕点
 按逆时针方向旋转,使
按逆时针方向旋转,使 落在射线
落在射线 上(如图(2)),则三角板旋转的角度为____度;
上(如图(2)),则三角板旋转的角度为____度;(2)继续将图2中的直角三角板绕点
 按逆时针方向旋转,使
按逆时针方向旋转,使 在
在 的内部(如图3).试求
的内部(如图3).试求 与
与 度数的差;
度数的差;(3)若图1中的直角三角板绕点
 按逆时针方向旋转一周,在此过程中:
按逆时针方向旋转一周,在此过程中:①当直角边
 所在直线恰好垂直于
所在直线恰好垂直于 时,
时,  的度数是________;
的度数是________;②设直角三角板绕点
 按每秒
按每秒 的速度旋转,当直角边
的速度旋转,当直角边 所在直线恰好平分
所在直线恰好平分 时,求三角板绕点
时,求三角板绕点 旋转时间
旋转时间 的值.
的值.
相关试题

