搜索
【题目】如图，将正方形纸片ABCD折叠，使点D落在边AB上的D'处，点C落在C'处，若∠AD'M=50°，则∠MNC'的度数为（ ）
A. 100°B. 110°C. 120°D. 130°
参考答案：
【答案】B
【解析】
折叠后，四边形CDMN与四边形C′D′MN关于MN对称，则∠DMN=∠D′MN，同时∠AMD′=90°-∠AD'M=40°，所以∠DMN=∠D′MN=（180°-40°）÷2=70°，根据四边形内角和360°即可求得∠MNC'的度数．
解：四边形CDMN与四边形C′D′MN关于MN对称，则∠DMN=∠D′MN，
且∠AMD′=90°-∠AD'M=40°，
∴∠DMN=∠D′MN=（180°-40°）÷2=70°
由于∠MD′C′=∠NC′D′=90°，
∴∠MNC'=360°-90°-90°-70°=110°
故选：B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某一天，小明和小亮来到一河边，想用遮阳帽和皮尺测量这条河的大致宽度，两人在确保无安全隐患的情况下，先在河岸边选择了一点B(点B与河对岸岸边上的一棵树的底部点D所确定的直线垂直于河岸)．
①小明在B点面向树的方向站好，调整帽檐，使视线通过帽檐正好落在树的底部点D处，如图所示，这时小亮测得小明眼睛距地面的距离AB＝1.7米；
②小明站在原地转动180°后蹲下，并保持原来的观察姿态(除身体重心下移外，其他姿态均不变)，这时视线通过帽檐落在了DB延长线上的点E处，此时小亮测得BE＝9.6米，小明的眼睛距地面的距离CB＝1.2米．
根据以上测量过程及测量数据，请你求出河宽BD是多少米？
-
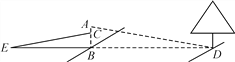
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知平行四边形ABCD与平行四边形DCFE的周长相等，且
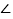BAD=60°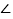，CFE=110°，则下列结论：①四边形ABFE为平行四边形；②
ADE是等腰三角形；③平行四边形ABCD与平行四边形DCFE全等；④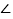DAE=25°.其中正确的结论是．__________(填正确结论的序号)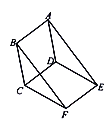
-
科目： 来源： 题型：
查看答案和解析>>【题目】能够铺满地面的正多边形组合是（ ）
A. 正三角形和正五边形B. 正方形和正六边形
C. 正方形和正五边形D. 正五边形和正十边形
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一副三角尺△ABC与△ADE的两条斜边在一条直线上，直尺的一边GF∥AC，则∠DFG的度数为_____________.
-
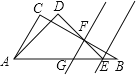
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD中，以对角线BD为一边构造一个矩形BDEF，使得另一边EF过原矩形的顶点C.
(1)设Rt△CBD的面积为S1，Rt△BFC的面积为S2，Rt△DCE的面积为S3，则S1__ __S2＋S3；(填“＞”“＝”或“＜”)
(2)写出图中的三对相似三角形，并选择其中一对进行证明．
-
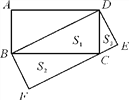
科目： 来源： 题型：
查看答案和解析>>【题目】选择适当的方法解下列方程：
（1）
；（2）
（3）
；（4）
.
相关试题
