【题目】如图,AB=AC,∠BAC=90°,BD⊥AE于D,CE⊥AE于E,且BD>CE.
求证:BD=EC+ED.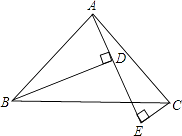
参考答案:
【答案】证明:∵∠BAC=90°,CE⊥AE,BD⊥AE,
∴∠ABD+∠BAD=90°,∠BAD+∠DAC=90°,∠ADB=∠AEC=90°.
∴∠ABD=∠DAC.
∵在△ABD和△CAE中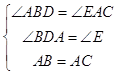 ,
,
∴△ABD≌△CAE(AAS).
∴BD=AE,EC=AD.
∵AE=AD+DE,
∴BD=EC+ED.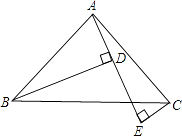
【解析】由题中AB=AC,以及AB和AC所在三角形为直角三角形,可以判断出应证明△ABD≌△CAE.
【考点精析】本题主要考查了全等三角形的性质的相关知识点,需要掌握全等三角形的对应边相等; 全等三角形的对应角相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a、b是方程x2+x-2020=0的两个不等实根,则a2+2a+b的值是_________.
-
科目: 来源: 题型:
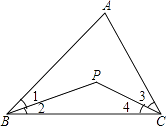
查看答案和解析>>【题目】如图,已知在△ABC中,∠B与∠C的平分线交于点P.当∠A=70°时,则∠BPC的度数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AD和BC相交于O,AB∥CD,∠AOC=95°,∠B=50°,求∠D.
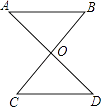
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列直线是圆的切线的是( )
A. 与圆有公共点的直线B. 到圆心的距离等于半径的直线
C. 垂直于圆的半径的直线D. 过圆直径外端点的直线
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程x2﹣6x+c=0有一个根为2,则另一根为( )
A.2
B.3
C.4
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).

(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈
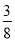 ,cos22°≈
,cos22°≈ ,tan22°≈
,tan22°≈ )
)
相关试题

