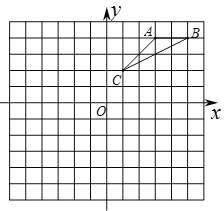
【题目】如图,△ABC三个顶点为A(3,4)、B(5,4)、C(1,2).请解答下列问题:
(1)画出△ABC关于y轴对称的△A1B1C1,使点A1与A对应,点B1与B对应;
(2)画出△ABC绕点O顺时针旋转90°后得到的△A2B2C2,使点A2与A对应,点B2与B对应;
(3)若△A1B1C1和△A2B2C2关于某直线对称,请直接写出该直线的解析式______________;
(4)直接写出△ABC的外心坐标_______________.
参考答案:
【答案】(1)图见解析;(2)图见解析;(3)y=x;(4)(4,1).
【解析】
(1)根据关于y轴对称的点的坐标特征写出A1,B1与C1点的坐标,然后描点即可;
(2)利用网格特点和旋转的性质画出A、B、C的对应点A2、B2、C2,从而得到△A2B2C2;
(3)利用所画图形可得到△A1B1C1和△A2B2C2关于第一、三象限的角平分线对称;
(4)作AB和AC的垂直平分线,它们的交点P为△ABC外接圆圆心,然后写出P点坐标即可.
(1)如图,△A1B1C1为所作;

(2)如图,△A2B2C2为所作;
(3)△A1B1C1和△A2B2C2关于直线y=x对称;
(4)△ABC外接圆圆心的坐标为(4,1).
故答案为y=x,(4,1).
-
科目: 来源: 题型:
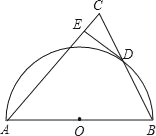
查看答案和解析>>【题目】如图,半圆O的直径为AB,D是半圆上的一个动点(不与点A,B重合),连接BD并延长至点C,使CD=BD,连接AC,过点D作DE⊥AC于点E.
(1)请猜想DE与⊙O的位置关系,并说明理由;
(2)当AB=4,∠BAC=45°时,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC为等边三角形,P是直线AC上一点,AD⊥BP于D,以AD为边作等边△ADE(D,E在直线AC异侧).
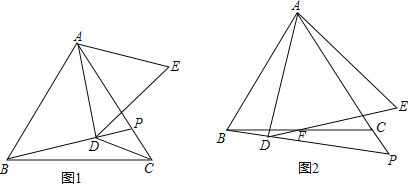
(1)如图1,若点P在边AC上,连CD,且∠BDC=150°,则
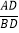 = ;(直接写结果)
= ;(直接写结果)(2)如图2,若点P在AC延长线上,DE交BC于F求证:BF=CF;
(3)在图2中,若∠PBC=15°,AB=
 ,请直接写出CP的长 .
,请直接写出CP的长 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是半圆
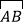 上一动点,以BC为边作正方形BCDE,使
上一动点,以BC为边作正方形BCDE,使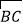 在正方形内,连OE,若AB=4cm,则OD的最大值为_____________cm.
在正方形内,连OE,若AB=4cm,则OD的最大值为_____________cm.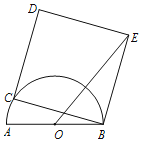
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线L1:y=
 x2-x-
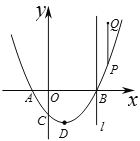
x2-x- ,L1交x轴于A,B(点A在点B左边),交y轴于C,其顶点为D,P是L1上一个动点,过P沿y轴正方向作线段PQ∥y轴,使PQ=t,当P点在L1上运动时,Q随之运动形成的图形记为L2.
,L1交x轴于A,B(点A在点B左边),交y轴于C,其顶点为D,P是L1上一个动点,过P沿y轴正方向作线段PQ∥y轴,使PQ=t,当P点在L1上运动时,Q随之运动形成的图形记为L2.(1)若t=3,求图形L2的函数解析式;
(2)过B作直线l∥y轴,若直线l和y轴及L1,L2所围成的图形面积为12,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】上周六上午
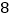 点,小颖同爸爸妈妈一起从西安出发回安康看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离
点,小颖同爸爸妈妈一起从西安出发回安康看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离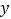 (千米)与他们路途所用的时间
(千米)与他们路途所用的时间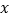 (时)之间的函数图象,请根据以上信息,解答下列问题:
(时)之间的函数图象,请根据以上信息,解答下列问题:(1)求直线
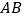 所对应的函数关系式;
所对应的函数关系式;(2)已知小颖一家出服务区后,行驶
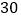 分钟时,距姥姥家还有
分钟时,距姥姥家还有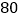 千米,问小颖一家当天几点到达姥姥家?
千米,问小颖一家当天几点到达姥姥家?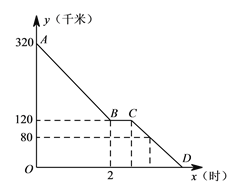
-
科目: 来源: 题型:
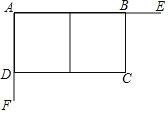
查看答案和解析>>【题目】如图,某工程队在工地互相垂直的两面墙AE、AF处,用180米长的铁栅栏围成一个长方形场地ABCD,中间用同样材料分割成两个长方形.已知墙AE长120米,墙AF长40米,要使长方形ABCD的面积为4000平方米,问BC和CD各取多少米?
相关试题

