【题目】在x轴上有点P(a,0)(其中a>2),过点P作x斜的蓬线,分别交函数 ![]() 和
和 ![]() 的图象于点C、D。
的图象于点C、D。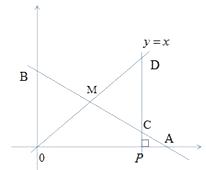
(1)求点A的坐标
(2)若OB=CD,求a的值
(3)在(2)条件下若以0D线段为边,作正方形0DEF,求直线EF的表达式。
参考答案:
【答案】
(1)解:∵点M在直线y=x的图象上,且点M的横坐标为2,
∴点M的坐标为(2,2),
把M(2,2)代入y=-![]() x+b得-1+b=2,解得b=3,
x+b得-1+b=2,解得b=3,
∴一次函数的解析式为y=-x+3,
把y=0代入y=-![]() x+3得-
x+3得-![]() x+3=0,解得x=6,
x+3=0,解得x=6,
∴A点坐标为(6,0);
(2)把x=0代入y=-1
2x+3得y=3,
∴B点坐标为(0,3),
∵CD=OB,
∴CD=3,
∵PC⊥x轴,
∴C点坐标为(a,-![]() a+3),D点坐标为(a,a)
a+3),D点坐标为(a,a)
∴a-(-![]() a+3)=3,
a+3)=3,
∴a=4.
(3)由(2)知,OD=4![]() ,∵四边形ODEF为正方形,∴EF
,∵四边形ODEF为正方形,∴EF![]() OD,且EF=OD,直线EF相当于直线OD向下平移8个单位得到的,∴直线EF 的表达式为y=x-8.
OD,且EF=OD,直线EF相当于直线OD向下平移8个单位得到的,∴直线EF 的表达式为y=x-8.
【解析】(1)先利用直线y=x上的点的坐标特征得到点M的坐标为(2,2),再把M(2,2)代入y=-1
2x+b可计算出b=3,得到一次函数的解析式为y=-![]() x+3,然后根据x轴上点的坐标特征可确定A点坐标为(6,0);
x+3,然后根据x轴上点的坐标特征可确定A点坐标为(6,0);
(2)先确定B点坐标为(0,3),则OB=CD=3,再表示出C点坐标为(a,-![]() a+3),D点坐标为(a,a),所以a-(-
a+3),D点坐标为(a,a),所以a-(-![]() a+3)=3,然后解方程即可
a+3)=3,然后解方程即可
(3)利用正方形的性质,OD 平行且等于EF,可利用平移关系求出EF的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中正确的是( )
A.3a+2a=5a2
B.(2a2)3=8a6
C.2a2a3=2a6
D.(2a+b)2=4a2+b2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB为⊙O的直径,BC⊥AB于B,且BC=AB,D为半圆⊙O上的一点,连接BD并延长交半圆⊙O的切线AE于E.
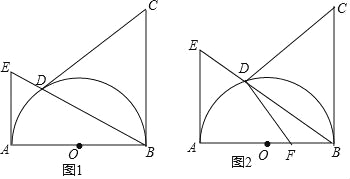
(1)如图1,若CD=CB,求证:CD是⊙O的切线;
(2)如图2,若F点在OB上,且CD⊥DF,求
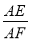 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.
(1)写出y与x中间的函数关系式和自变量
 的取值范围;
的取值范围;(2)超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从下列四个条件:①BC=B′C;②AC=A′C;③∠A′CA=∠B′CB;④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )

A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】类比学习:一动点沿着数轴先向右平移3个单位长度,再向左平移2个单位长度,相当于向右平移1个单位长度.用实数加法表示为3+(-2)=1.若坐标平面上的点有如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移|a|个单位长度),沿y轴方向平移的数量为b(向上为正,向下为负,平移|b|个单位长度),则把有序数对{a,b}叫做这一平移的“平移量”,“平移量”{a,b}与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}={a+c,b+d}.
解决问题:
(1)计算:{3,1}+{1,2},{1,2}+{3,1}.
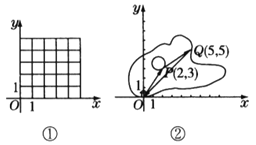
(2)动点P从坐标原点O出发,先按照“平移量”{3,1}平移到点A,再按照“平移量”{1,2}平移到点B;若先把动点P按照“平移量”{1,2}平移到点C,再按照“平移量”{3,1}平移,最后的位置还是点B吗?在图①中画出四边形OABC.
(3)如图②所示,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O.请用“平移量”加法算式表示它的航行过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】24表示( )
A.2×2×2×2B.2×4 C.4×4 D.2+2+2+2
相关试题

