【题目】如图,已知数轴上的三点A、B、C,点A表示的数为5,点B表示的数为-3,点C到点A、点B的距离相等,动点P从点A出发,以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.
(1)点C在数轴上表示的数是______;
(2)当t=______秒时,点P到达点B处:
(3)用含字母t的代数式表示线段AP=______;点P在数轴上表示的数是______.
(4)当P,C之间的距离为1个单位长度时,求t的值.
![]()
参考答案:
【答案】(1)1 ;(2) 4 ;(3) 2t 5-2t;(4)t=1.5或2.5.
【解析】
(1)计算AB长度,根据点C到点A、点B的距离相等可确定C表示数字;
(2)P运动路程是8,然后除以速度求解;
(3)根据路程等于速度乘以时间来表示AP长度,用点A表示数字减点AP长度即点P表示数字;
(4)分P在C左右两边两种可能列式求解.
解:(1)AB=5-(-3)=8,
8÷2=4,
5-4=1.
故答案为:1;
(2)8÷2=4,
故答案为:4;
(3)AP=2t,
所以P表示的数是5-2t,
故答案为:2t,5-2t;
(4)P在C右边时,5-2t-1=1,
解得t=1.5;
P在C左边时,1-(5-2t)=1,
解得t=2.5,
所以当t=1.5或2.5秒时P,C之间的距离为1个单位长度.
故答案为:(1)1 ;(2) 4 ;(3) 2t 5-2t;(4)t=1.5或2.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的两边分别是2cm和3cm,现从长度分别为1cm、2cm、3cm、4cm、5cm、6cm六根小木棒中随机抽一根,抽到的木棒能作为该三角形第三边的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某人到岛上去探宝,从A处登陆后先往东走4 km,又往北走1.5 km,遇到障碍后又往西走2 km,再折回向北走到4.5 km处往东一拐,仅走0.5 km就找到宝藏.问登陆点A与宝藏埋藏点B之间的距离是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】新农村社区改造中,有一部分楼盘要对外销售,某楼盘共23层,销售价格如下:第八层楼房售价为4000元/米2,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,已知该楼盘每套楼房面积均为120米2.
若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价8%,另外每套楼房赠送a元装修基金;
方案二:降价10%,没有其他赠送.
(1)请写出售价y(元/米2)与楼层x(1≤x≤23,x取整数)之间的函数关系式;
(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】折叠矩形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆柱底面半径为
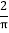 cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )A. 12cm B.
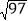 cm C. 15cm D.
cm C. 15cm D. 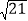 cm
cm -
科目: 来源: 题型:
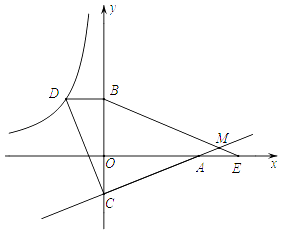
查看答案和解析>>【题目】如图,已知点D在反比例函数y=
 的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=
的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC= 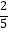 .
.
(1)求反比例函数y= 和直线y=kx+b的解析式;
和直线y=kx+b的解析式;
(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA与点M,求∠BMC的度数.
相关试题

