【题目】在数-5,1,-3,5,-2中任取三个数相乘,其中最小的积是 .
参考答案:
【答案】-30
【解析】在数-5,1,-3,5,-2中任取三个数相乘,共有以下几种情况:
(-5)![]() 1
1![]() (-3)=15;
(-3)=15;
(-5)![]() 1
1![]() 5=-25;
5=-25;
(-5)![]() 1
1![]() (-2)=10;
(-2)=10;
(-5)![]() (-3)
(-3)![]() 5=75;
5=75;
(-5) × (-3) ×(-2)=-30;
(-5) × 5 ×(-2)=50;
1 × (-3) ×5=-15;
1 × (-3) ×(-2)=6;
1 × 5 ×(-2)=-10;
(-3) ×5 ×(-2)=30.
∴其中最小的积是-30.
所以答案是:-30.
【考点精析】解答此题的关键在于理解有理数的乘法法则的相关知识,掌握有理数乘法法则:1、两数相乘,同号为正,异号为负,并把绝对值相乘2、任何数同零相乘都得零3、几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上A点表示数a,B点表示数b,C点表示数c,且a、c满足|a+3|+(c﹣9)2=0.
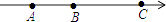
(1)a= , c=;
(2)如图所示,在(1)的条件下,若点A与点B之间的距离表示为AB=|a﹣b|,点B与点C之间的距离表示为BC=|b﹣c|,点B在点A、C之间,且满足BC=2AB,则b=;
(3)在(1)(2)的条件下,若点P为数轴上一动点,其对应的数为x,当代数式|x﹣a|+|x﹣b|+|x﹣c|取得最小值时,此时x= , 最小值为;
(4)在(1)(2)的条件下,若在点B处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点C处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),请表示出甲、乙两小球之间的距离d(用t的代数式表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算错误的是( )
A.a8÷a4=a4B.(a2b)4=a8b4
C.a2+a2=2a2D.(a3)2=a5
-
科目: 来源: 题型:
查看答案和解析>>【题目】设计一张折叠型方桌子如图,若AO=BO=50cm,CO=DO=30cm,将桌子放平后,要使AB距离地面的高为40cm,则两条桌腿需要叉开的∠AOB应为( )
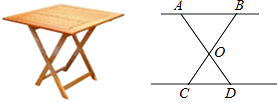
A.60°
B.90°
C.120°
D.150° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图A、B分别为数轴上的两点,A点对应的数为-10,B点对应的数为70.
(1)请写出AB的中点M对应的数
(2)现在有一只电子蚂蚁P从A点出发,以3个单位/秒的速度向右运动,同时另一只电子蚂蚁Q恰好从B点出发,以2个单位/秒的速度向左运动,设两只电子蚂蚁在数轴上的C点相遇,请你求出C点对应的数
(3)若当电子蚂蚁P从A点出发,以3个单位/秒的速度向右运动,同时另一只电子蚂蚁Q恰好从B点出发,以2单位/秒的速度向左运动,经过多长时间两只电子蚂蚁在数轴上相距35个单位长度,并写出此时P点对应的数. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一家苗圃计划植桃树和柏树,根据市场调查与预测,种植桃树的利润
 (万元)与投资成本x(万元)满足如图①所示的二次函数
(万元)与投资成本x(万元)满足如图①所示的二次函数 ;种植柏树的利润
;种植柏树的利润 (万元)与投资成本x(万元)满足如图②所示的正比例函数
(万元)与投资成本x(万元)满足如图②所示的正比例函数 =kx.
=kx.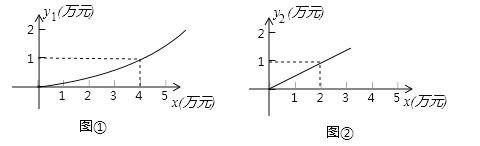
(1)分别求出利润
 (万元)和利润
(万元)和利润 (万元)关于投资成本x(万元)的函数关系式;
(万元)关于投资成本x(万元)的函数关系式;(2)如果这家苗圃以10万元资金投入种植桃树和柏树,桃树的投资成本不低于2万元且不高于8万元,苗圃至少获得多少利润?最多能获得多少利润?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各对数中,相等的一对数是( )
A.(﹣2)3与﹣23
B.﹣22与(﹣2)2
C.﹣(﹣3)与﹣|﹣3|
D.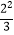 与(
与(  )2
)2
相关试题

