【题目】如图,点![]() 是正方形
是正方形![]() 对角线
对角线![]() 上一点,
上一点,![]() 于
于![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.
的中点.
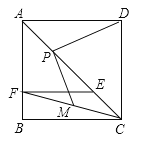
(1)求证:![]() ;
;
(2)当点![]() 在对角线
在对角线![]() (不含
(不含![]() 、
、![]() 两点)上运动时,
两点)上运动时,![]() 是否为定值?如果是,请求其值;如果不是,试说明理由.
是否为定值?如果是,请求其值;如果不是,试说明理由.
参考答案:
【答案】(1)证明见解析;(2)是定值,![]()
【解析】
(1)首先证明△AFE是等腰直角三角形,可得PF⊥AE,由直角三角形的性质可得结论;
(2)由“SAS”可证△APB≌△APD,可得PB=PD,通过证明△AFC∽△APB,可得![]() ,即可得
,即可得![]() .
.
解:(1)如图,连接PF,
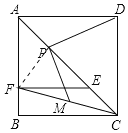
∵四边形ABCD是正方形
∴∠BAC=45°=∠CAD,AB=AD
∵EF⊥AB
∴∠BAC=∠AEF=45°
∴AF=EF,
∴△AFE是等腰直角三角形,且P是AE中点,
∴PF⊥AE,
∵点M是Rt△PFC斜边FC的中点
∴PM=![]() FC
FC
(2)是定值,
理由如下:如图,连接PB
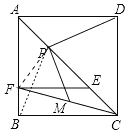
∵AP=AP,∠BAC=∠DAC=45°,AB=AD
∴△APB≌△APD(SAS)
∴PD=PB
∵△ABC,△AFE是等腰直角三角形
∴![]() ,
,![]()
∴![]() ,且∠BAP=∠FAC
,且∠BAP=∠FAC
∴△AFC∽△APB
∴![]()
∴![]()
∴![]()
-
科目: 来源: 题型:
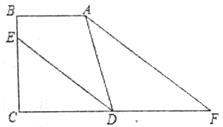
查看答案和解析>>【题目】如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF.求证:∠DAF=∠F.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,
 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】小丽购买学习用品的收据如表,因污损导致部分数据无法识别,根据下表,解决下列问题:
(1)小丽买了自动铅笔、记号笔各几支?
(2)若小丽再次购买软皮笔记本和自动铅笔两种文具,共花费15元,则有哪几种不同的购买方案?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形
 中,
中, .
.
(1)如图1,点
 为线段
为线段 的中点,连接
的中点,连接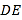 ,
, .若
.若 ,求线段
,求线段 的长.
的长.(2)如图2,
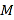 为线段
为线段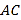 上一点(不与
上一点(不与 ,
, 重合),以
重合),以 为边向上构造等边三角形
为边向上构造等边三角形 ,线段
,线段 与
与 交于点
交于点 ,连接
,连接 ,
, ,
, 为线段
为线段 的中点.连接
的中点.连接 ,
, 判断
判断 与
与 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.(3)在(2)的条件下,若
 ,请你直接写出
,请你直接写出 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点
 ,点
,点 ,以
,以 为边在右侧作正方形
为边在右侧作正方形

(1)当点
 在
在 轴正半轴上运动时,求点
轴正半轴上运动时,求点 的坐标(用
的坐标(用 表示);
表示);(2)当
 时,如图2,
时,如图2, 为
为 上一点,过点
上一点,过点 作
作 ,
, ,连
,连 交
交 于点
于点 ,求
,求 的值;
的值;(3)如图3,在第(2)问的条件下,
 、
、 分别为
分别为 、
、 上的点,作
上的点,作 轴交
轴交 于
于 ,作
,作 轴交
轴交 于
于 ,
, 是
是 与
与 的交点,若
的交点,若 ,试确定
,试确定 的大小,并证明你的结论.
的大小,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O是坐标原点,ABCD的顶点A的坐标为(﹣2,0),点D的坐标为(0,2
 ),点B在x轴的正半轴上,点E为线段AD的中点.
),点B在x轴的正半轴上,点E为线段AD的中点.(Ⅰ)如图1,求∠DAO的大小及线段DE的长;
(Ⅱ)过点E的直线l与x轴交于点F,与射线DC交于点G.连接OE,△OEF′是△OEF关于直线OE对称的图形,记直线EF′与射线DC的交点为H,△EHC的面积为3
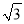 .
.①如图2,当点G在点H的左侧时,求GH,DG的长;
②当点G在点H的右侧时,求点F的坐标(直接写出结果即可).

相关试题

